Giải câu 63 bài 8: Các trường hợp bằng nhau của tam giác vuông sgk Toán 7 tập 1 Trang 136

Câu 63 : Trang 136 - sgk toán 7 tập 1

Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC(H thuộc BC). Chứng minh rằng:

a) HB = HC;

b) = \(\widehat{CAH}\)

Bài làm:

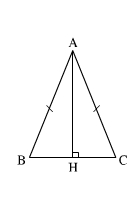
a) Xét tam giác vuông ABH và tam giác vuông ACH có:

AB = AC (giả thiết)

AH cạnh chung.

=> ∆ABH = ∆ACH(Cạnh huyền - cạnh góc vuông)

=> HB = HC (cạnh tương ứng) (đpcm)

b)Do ∆ABH = ∆ACH (Chứng minh trên)

=> = \(\widehat{CAH}\) (góc tương ứng) (đpcm)