Giải Câu 7 Bài Ôn tập cuối năm

Câu 7: Trang 126 - SGK Hình học 11

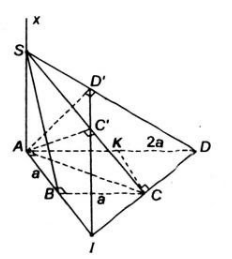
Cho hình thang vuông tại \(A\) và \(B\), có \(AD = 2a, AB = BC = a\). Trên tia \(Ax\) vuông góc với mặt phẳng \((ABCD)\) lấy một điểm \(S\). Gọi \(C',D'\) lần lượt là hình chiếu vuông góc của \(A\) trên \(SC\) và \(SD\) . Chứng minh rằng :

a)

b) và \(AB\) cùng nằm trên một mặt phẳng.

c) Chứng minh rằng đường thẳng luôn luôn đi qua một điểm cố định khi \(S\) di động trên tia Ax.

Bài làm:

a) Chứng minh

Ta có: \(\left. \matrix{
SA \bot \left( {ABC{\rm{D}}} \right) \hfill \cr
AB \bot BC \hfill \cr} \right\} \Rightarrow SB \bot BC\) (định lí 3 đường vuông góc)

Gọi là trung điểm của \(AD\).

là hình vuông nên \(CK = a \Rightarrow CK = {1 \over 2}A{\rm{D}}\)

Tam giác ACD có trung tuyến CK bằng cạnh tương ứng nên ACD là tam giác vuông tại C

=> AC CD

\(\left. \matrix{
SA \bot \left( {ABC{\rm{D}}} \right) \hfill \cr
AC \bot C{\rm{D}} \hfill \cr} \right\} \Rightarrow SC \bot C{\rm{D}}\) (định lí 3 đường vuông góc)

b) Ta có :

\(\left. \matrix{
AB \bot SA \hfill \cr
AB \bot A{\rm{D}} \hfill \cr} \right\} \Rightarrow \left. \matrix{
AB \bot \left( {SA{\rm{D}}} \right) \hfill \cr
S{\rm{D}} \subset \left( {SA{\rm{D}}} \right) \hfill \cr} \right\} \Rightarrow AB \bot S{\rm{D}}(1)\)

\(\left. \matrix{
C{\rm{D}} \bot AC \hfill \cr
C{\rm{D}} \bot SC \hfill \cr} \right\} \Rightarrow \left. \matrix{
C{\rm{D}} \bot \left( {SAC} \right) \hfill \cr
AC' \subset \left( {SAC} \right) \hfill \cr} \right\} \Rightarrow AC' \bot C{\rm{D}}\)

Kết hợp với AC’ SC suy ra AC' (SCD)

Vậy

\(\left. \matrix{
AC' \bot \left( {SC{\rm{D}}} \right) \hfill \cr
S{\rm{D}} \subset \left( {SC{\rm{D}}} \right) \hfill \cr} \right\} \Rightarrow AC' \bot S{\rm{D(2)}}\)

Giả thiết cho AD’ SD (3)

Từ (1), (2), (3) ta thấy ba đường thẳng AB, AD’, AC’ cùng vuông góc với SC. Vậy chúng cùng nằm trong mặt phẳng ( P) đi qua A và vuông góc với SC.

c) Gọi I là giao điểm của C’D’ với AB.

⇒ I là giao điểm của hai mặt phẳng (SCD) và (ABCD)

Hai mặt phẳng này cắt nhau theo giao tuyến CD. Như vậy ba đường thẳng AB, CD, C’D’ đồng quy tại I và AB, CD cố định suy ra I cố đinh.

Khi S chạy trên Ax thì C’D’ luôn đi qua điểm cố định là giao điểm I của AB và CD