Giải câu 70 bài Ôn tập chương II Tam giác sgk Toán 7 tập 1 Trang 141

Câu 70 : Trang 141 - sgk toán 7 tập 1

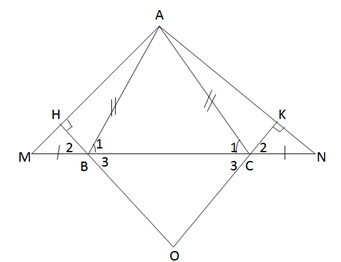
Cho tam giác ABC cân tại A. Trên tia đối của BC lấy điểm M, trên tia đối của tia CB lấy điểm N sao cho BM = CN.

a) Chứng minh rằng tam giác AMN là tam giác cân.

b) Kẻ BH ⊥ AM (H thuộc AM), kẻ CK ⊥ AN (K thuộc AN). Chứng minh rằng BH = CK.

c) Chứng minh rằng AH = AK.

d) Gọi O là giao điểm của HB và KC. Tam giác OBC là tam giác gì? Vì sao ?

e) Khi và BM = CN = BC, hãy tính số đo các góc của tam giác AMN và xác định dạnh của tam giác OBC.

Bài làm:

a) ∆ABC cân, suy ra

mà kề bù với góc $\widehat{ABM}$ và $\widehat{C_1}$ kề bù với góc $\widehat{ACN}$

Xét ∆ABM và ∆CAN có:

AB = AC (do tam giác ABC cân tại A)

(cmt)

BM = ON (gỉa thiết)

=>∆ABM = ∆CAN (c.g.c)

=>AM = AN (cạnh tương ứng)

=>∆AMN là tam giác cân ở A (đpcm)

b) Do ∆ABM = ∆CAN (c.g.c)

=>

Xet tam giác vuông ∆BHA và tam giác vuông ∆CKA có :

AB = AC (giả thiết)

(cmt)

=> ∆BHA = ∆CHA (cạnh huyền, góc nhọn)

=> BH = CK. (cạnh tương ứng)

c) Câu b ta chứng minh được:

∆BHA = ∆CHA => AH =AK (cạnh tương ứng)

d) Do tam giác AMN cân =>

Xét ∆BHM và ∆CKN có:

CN = BM (giả thiết)

=> ∆BHM = ∆CKN (cạnh huyền - góc nhọn)

=> (góc tương ứng)

Mà (hai góc đối đỉnh)

=> .

Vậy ∆OBC là tam giác cân.

e) Tam giác cân ABC có nên là tam giác đều.

=> AB = BC = AC = BM = CN

(cùng bù với 60⁰)

Do AB = BM (chứng minh trên ) => ∆ABM cân ở B

=> .

=>Trong tam giác AMN có:

.

Trong ∆BHM có:

=> (hai góc phụ nhau)

=>

Tương tự

=>Tam giác OBC có:

nên tam giác OBC là tam giác đều.