Trắc nghiệm đại số 10 chương 4: Bất đẳng thức, bất phương trình (P2)

Bài có đáp án. Bộ bài tập trắc nghiệm toán 10 đại số chương 4: Bất đẳng thức, bất phương trình (P2). Học sinh luyện tập bằng cách chọn đáp án của mình trong từng câu hỏi. Dưới cùng của bài trắc nghiệm, có phần xem kết quả để biết bài làm của mình. Kéo xuống dưới để bắt đầu.

Câu 1: Cho biểu thức . Tập hợp tất cả các giá trị của x thỏa mãn bất phương trình f(x) ≥ 0 là:

• A. x ∈ (− ∞; −2] ∪ [2; 4)
• B. x ∈ (3; + ∞)
• C. x ∈ (− 2; 4)
• D. x ∈ (− 2; 2) ∪ (4; + ∞)

Câu 2: Biểu thức âm khi

• A. x ∈ (1; 2)
• B. x ∈ (−3; −2) ∪ (1; 2)
• C. x ≥ 4
• D. x ∈ (−∞; −3) ∪ (−2; 1) ∪ (2; +∞)

Câu 3: Gọi S là tập nghiệm của bất phương trình −2 ≤ x ≤ 4. Chọn mệnh đề đúng:

• A. S = {−2; −1; 0; 1; 2; 3; 4}
• B. {0} ∈ S
• C. S = [−2; 4]
• D. S = {−2; 4}

Câu 4: Phương trình − (m + 1)x + 1 = 0 vô nghiệm khi và chỉ khi

• A. m > 1
• B. − 3 < m < 1
• C. m ≤ − 3 hoặc m ≥ 1
• D. − 3 ≤ m ≤ 1

Câu 5: Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương trình nào trong bốn hệ A, B, C, D?

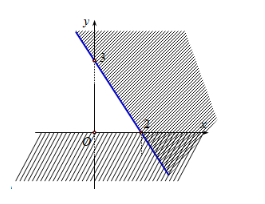
• A.
• B.
• C.
• D.

Câu 6: Để bất phương trình nghiệm đúng ∀x ∈ [−5; 3], tham số a phải thỏa mãn điều kiện:

• A. a ≥ 3
• B. a ≥ 4
• C. a ≥ 5
• D. a ≥ 6

Câu 7: Giá trị nhỏ nhất của hàm số f(x) = 2x + với x > 0 là

• A. 4
• B.
• C. 2
• D. 2

Câu 8: Giá trị nhỏ nhất của biểu thức F = y − x trên miền xác định bởi hệ là

• A. minF = 1 khi x = 2, y = 3
• B. minF = 2 khi x = 0, y = 2
• C. minF = 3 khi x = 1, y = 4
• D. minF = 0 khi x = 0, y = 0

Câu 9: Cặp bất phương trình nào sau đây là tương đương?

• A. x − 2 ≤ 0 và (x − 2) ≤ 0
• B. x − 2 < 0 và (x − 2) > 0
• C. x − 2 < 0 và (x − 2) < 0
• D. x − 2 ≥ 0 và (x − 2) ≥ 0

Câu 10: Phương trình + 2(m + 2)x − 2m − 1 = 0 (m là tham số) có hai nghiệm phân biệt khi

• A. m = −1 hoặc m = −5
• B. − 5 ≤ m ≤ − 1
• C. m < − 5 hoặc m > −1
• D. m ≤ − 5 hoặc m ≥ − 1

Câu 11: Hỏi bất phương trình (2 − x)(x + 1)(3 − x) ≤ 0 có tất cả bao nhiêu nghiệm nguyên dương ?

• A. 1
• B. 3
• C. 4
• D. 2

Câu 12: Tập nghiệm S của bất phương trình là:

• A. S = (−∞; 3)
• B. S = (3; +∞)
• C. S = [3; +∞)
• D. S = (−∞; 3]

Câu 13: Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24g hương liệu, 9 lít nước và 210g đường để pha

chế nước cam và nước táo.

+ Để pha chế 1 lít nước cam cần 30g đường, 1 lít nước và 1g hương liệu;

+ Để pha chế 1 lít nước táo cần 10g đường, 1 lít nước và 4g hương liệu.

Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Hỏi cần pha chế bao

nhiêu lít nước trái cây mỗi loại để đạt được số điểm thưởng cao nhất?

• A. 5 lít nước cam và 4 lít nước táo
• B. 6 lít nước cam và 5 lít nước táo
• C. 4 lít nước cam và 5 lít nước táo
• D. 4 lít nước cam và 6 lít nước táo

Câu 14: Xác định m để với mọi x ta có .

• A. − ≤ m < 1
• B. 1 < m ≤
• C. m ≤ −
• D. m < 1

Câu 15: Cho x, y là hai số thực thỏa mãn x > y và xy = 1000. Biết biểu thức đạt giá trị nhỏ nhất khi $\left\{\begin{matrix}x = a\\ y = b \end{matrix}\right.$. Tính $\frac{a^{2} + b^{2}}{1000}$

• A. P = 2
• B. P = 3
• C. P = 4
• D. P = 5

Câu 16: Bất phương trình: |3x − 3| ≤ |2x + 1| có nghiệm là:

• A. [4; + ∞)
• B. (− ∞; ]
• C. [; 4]
• D. (−∞; 4]

Câu 17: Tìm các giá trị thực của tham số m để phương trình (m − 1) − 2mx + m = 0 có một nghiệm lớn hơn 1 và một nghiệm nhỏ hơn 1?

• A. 0 < m < 1
• B. m > 1
• C. m ∈ ∅
• D.

Câu 18: Số nghiệm của phương trình là

• A. 2
• B. 3
• C. 0
• D. 1

Câu 19: Tìm tất cả các giá trị thực của tham số m để bất phương trình (x + m)m + x > 3x + 4 có tập nghiệm là (−m − 2; +∞).

• A. m = 2
• B. m ≠ 2
• C. m > 2
• D. m < 2

Câu 20: Hỏi có bao nhiêu giá trị nguyên x thỏa mãn bất phương trình ?

• A. 1
• B. 2
• C. 4
• D. 3