Trắc nghiệm hình học 10 chương 2: Tích vô hướng của hai vecto và ứng dụng (P1)

Bài có đáp án. Bộ bài tập trắc nghiệm hình học 10 chương 2: Tích vô hướng của hai vecto và ứng dụng (P1). Học sinh luyện tập bằng cách chọn đáp án của mình trong từng câu hỏi. Dưới cùng của bài trắc nghiệm, có phần xem kết quả để biết bài làm của mình. Kéo xuống dưới để bắt đầu.

Câu 1: Trong các đẳng thức sau đây, đẳng thức nào đúng?

• A. sin(180 − α) = −sinα
• B. cos(180 − α) = cosα
• C. tan(180 − α) = tanα
• D. cot(180 − α) = −cotα

Câu 2: Trong mặt phẳng Oxy cho A(4; 6), B(1; 4), . Khẳng định nào sau đây sai

• A.
• B. = 0
• C.
• D.

Câu 3: Cho hình thang vuông ABCD có đáy lớn AB = 4a, đáy nhỏ CD = 2a, đường cao AD = 3a; I là trung điểm của AD. Khi đó bằng:

• A.
• B.
• C. 0
• D.

Câu 4: Giá trị của E = là:

• A.
• B.
• C. 1
• D. -1

Câu 5: Cho hai điểm A(−3, 2), B(4, 3). Tìm điểm M thuộc trục Ox và có hoành độ dương để tam giác MAB vuông tại M

• A. M(7; 0)
• B. M(5; 0)
• C. M(3; 0)
• D. M(9; 0)

Câu 6: Cho hai vectơ và $\vec{b}$ khác $\vec{0}$. Xác định góc giữa hai vectơ và $\vec{B}$ khi $\vec{a}.\vec{b}$ = -$|\vec{a}|.|\vec{b}|$.

• A. α =
• B. α =
• C. α =
• D. α =

Câu 7: Cho hình vuông ABCD cạnh a. Hỏi mệnh đề nào sau đây là sai?

• A.
• B.
• C.
• D.

Câu 8: Cho đường tròn tâm O bán kính R và điểm M thỏa mãn MO = 3R. Một đường kính AB thay đổi trên đường tròn. Giá trị nhỏ nhất của biểu thức S = MA + MB.

• A. minS = 6R
• B. minS = 4R
• C. minS = 2R
• D. minS = R

Câu 9: Tam giác ABC có BC = 10 và . Khi đó, bán kính đường tròn ngoại tiếp tam giác ABC là:

• A. 5
• B. 10
• C.
• D.

Câu 10: Cho tam giác đều ABC với cạnh a, với các đường cao AH, BK; vẽ . Câu nào sau đây là đúng?

• A.
• B.
• C.
• D. cả 3 câu trên

Câu 11: Trong các đẳng thức sau đây, đẳng thức nào đúng?

• A. sin150 = -$\frac{\sqrt{3}}{2}$
• B. cos150 = $\frac{\sqrt{3}}{2}$
• C. tan150 = $\frac{-1}{\sqrt{3}}$
• D. cot150 = $\sqrt{3}$

Câu 12: Trong mặt phẳng tọa độOxy, cho bốn điểm A(−8; 0), B(0; 4), C(2; 0), D(−3; −5). Khẳng định nào sau đây là đúng?

• A. Hai góc và $\widehat{BCD}$ phụ nhau.
• B. Góc là góc nhọn.
• C. cos() = cos($\vec{CB}, \vec{CD}$)
• D. Hai góc BˆAD và BˆCD bù nhau.

Câu 13: Biết cosa = và $90^{\circ} < a < 180^{\circ}$. Tính tana?

• A.
• B.
• C.
• D.

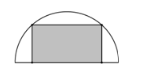
Câu 14: Từ một miếng tôn có hình dạng là nửa đường tròn bán kính 1m, người ta cắt ra một hình chữ nhật. Hỏi có thể cắt được miếng tôn có diện tích lớn nhất là bao nhiêu?

• A. 1,6
• B. 2
• C. 1
• D. 0,8

Câu 15: Cho tam giác ABC có AB = 8cm, AC = 18cm và có diện tích bằng . Giá trị của sin$\widehat{A}$ là:

• A.
• B.
• C.
• D.

Câu 16: Trong mặt phẳng tọa độ Oxy cho A(3; −1), B −1; 2) và I(1; −1). Gọi C, D là các điểm sao cho tứ giác ABCD là hình bình hành, biết I là trọng tâm tam giác. Tìm tọa tâm O của hình bình hành ABCD.

• A. O (3; −)
• B. O (2; −)
• C. O (−2; −)
• D. O (2; )

Câu 17: Giá trị của biểu thức A = là

• A. 0
• B. 2
• C.
• D. 1

Câu 18: Cho hình bình hành ABCD có AB = a, BC = a và $\widehat{BAD} = 45^{\circ}$. Khi đó hình bình hành có diện tích bằng:

• A. 2
• B.
• C.
• D.

Câu 19: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A (6; 0), B(3; 1) và C(−1; −1). Tính số đo góc B của tam giác đã cho.

• A.
• B.
• C.
• D.

Câu 20: Cho hình bình hành ABCD có AD = 4 và chiều cao ứng với cạnh AD bằng 3, . Chọn hệ trục toạ độ (A,$\vec{i}, \vec{j}$) sao cho $\vec{i}$ và $\vec{AD}$ cùng hướng, $y_{B} > 0$. Tìm khẳng định sai?

• A.
• B.
• C.
• D.