Đáp án câu 5 đề 9 kiểm tra học kì 2 toán 7

Câu 5: Cho tam giác ABC có AB= 6cm, AC= 12cm, BC= 15cm

a. Chứng minh rằng tam giác ABC vuông

b. Vẽ trung tuyến AM. Từ M vẽ MH vuông góc với AC. Trên tia đối của tia MH lấy điểm K sao cho MK = MH. Chứng minh

c. Gọi G là giao điểm của BH và AM. Gọi I là trung điểm của AB. Chứng minh I, G, C thẳng hàng

Bài làm:

Câu 5:

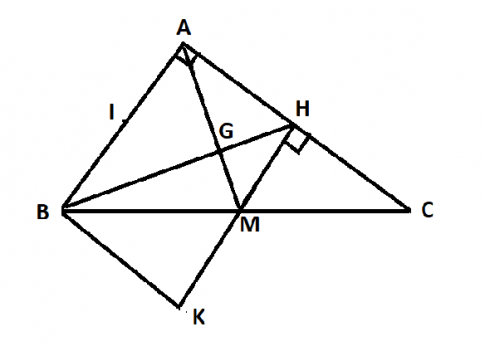
a. Ta có

ttheo định lý Pitago đảo thì tam giác ABC vuông tại A

b. Xét tam giác MHC và tam giác MKB có:

MC = MB (gt)

(đối đỉnh)

MH = MK (gt)

Do đó (c.g.c)

c. Ta có trung tuyến hay AM = MC nên tam giác AMC cân tại M.

Trong tam giác AMC có đường cao MH nên MH cũng là đường trung tuyến hay H là trung điểm của AC

=> BH là đường trung tuyến của tam giác ABC

mà BH giao AM tại G nên G là trọng tâm của tam giác ABC

Trong tam giác ABC có I là trung điểm của AB nên Ci là trung tuyến lại có G là trọng tâm nên CI phải đi qua G

=> I, G, C thẳng hàng