Giải câu 1 trang 101 toán VNEN 7 tập 1
C. Hoạt động luyện tập
Câu 1: Trang 101 toán VNEN 7 tập 1
a) Cho định lí: Góc tạo bởi hai tia phân giác của hai góc kề bù là một góc vuông.
- Hãy cho biết giả thiết của định lí.
- Hãy cho biết kết luận của định lí.
- Hãy chứng minh định lí trên.
b) Cho định lí: Nếu một đường thẳng cắt hai đường thẳng phân biệt và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì các góc đồng vị bằng nhau.
- Hãy cho biết giả thiết của định lí.
- Hãy cho biết kết luận của định lí.
- Hãy chứng minh định lí trên.
Bài làm:
a)
- Giả thiết của định lí là: "góc tạo bởi hai tia phân giác của hai góc kề bù".
- Kết luận của định lí là: "một góc vuông".
- Chứng minh định lí:
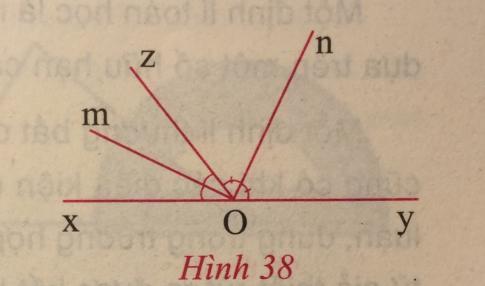
Có ![]() và $\widehat{zOy}$ là hai góc kề bù. Om là tia phân giác của
và $\widehat{zOy}$ là hai góc kề bù. Om là tia phân giác của ![]() và On là tia phân giác của $\widehat{zOy}$.
và On là tia phân giác của $\widehat{zOy}$.
Ta có: ![]() = $\frac{1}{2}$$\widehat{xOz}$; $\widehat{nOz}$ = $\frac{1}{2}$$\widehat{yOz}$, mà $\widehat{xOz}$ + $\widehat{yOz}$ = 180$^{0}$.
= $\frac{1}{2}$$\widehat{xOz}$; $\widehat{nOz}$ = $\frac{1}{2}$$\widehat{yOz}$, mà $\widehat{xOz}$ + $\widehat{yOz}$ = 180$^{0}$.
![]() $\widehat{mOz}$ + $\widehat{nOz}$ = 90$^{0}$.
$\widehat{mOz}$ + $\widehat{nOz}$ = 90$^{0}$.
b)
- Giả thiết của định lí là: "một đường thẳng cắt hai đường thẳng phân biệt và trong các góc tạo thành có một cặp góc so le trong bằng nhau".
- Kết luận của định lí là: "các góc đồng vị bằng nhau".
- Chứng minh định lí:
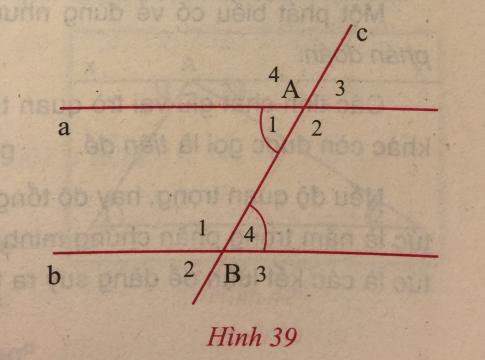
Giả sử đường thẳng c cắt hai đường thẳng phân biệt a và b tương ứng tại các điểm A và B, đồng thời có ![]() = $\widehat{B_{4}}$.
= $\widehat{B_{4}}$.
Ta có: ![]() và $\widehat{A_{3}}$ là hai góc đối đỉnh nên
và $\widehat{A_{3}}$ là hai góc đối đỉnh nên ![]() = $\widehat{A_{3}}$, mà
= $\widehat{A_{3}}$, mà ![]() = $\widehat{B_{4}}$ (giả thiết)
= $\widehat{B_{4}}$ (giả thiết)
![]() $\widehat{A_{3}}$ = $\widehat{B_{4}}$.
$\widehat{A_{3}}$ = $\widehat{B_{4}}$.
Mặt khác, ![]() và $\widehat{A_{2}}$ là hai góc kề bù nên
và $\widehat{A_{2}}$ là hai góc kề bù nên ![]() + $\widehat{A_{2}}$ = 180$^{0}$, tương tự, $\widehat{B_{3}}$ + $\widehat{B_{4}}$ = 180$^{0}$, mà
+ $\widehat{A_{2}}$ = 180$^{0}$, tương tự, $\widehat{B_{3}}$ + $\widehat{B_{4}}$ = 180$^{0}$, mà ![]() = $\widehat{B_{4}}$ (giả thiết)
= $\widehat{B_{4}}$ (giả thiết)
![]() $\widehat{A_{2}}$ = $\widehat{B_{3}}$.
$\widehat{A_{2}}$ = $\widehat{B_{3}}$.
Tương tự, ![]() và $\widehat{A_{4}}$ là hai góc đối đỉnh nên
và $\widehat{A_{4}}$ là hai góc đối đỉnh nên ![]() = $\widehat{A_{4}}$, mà $\widehat{A_{4}}$ = $\widehat{B_{1}}$, từ đó suy ra $\widehat{A_{4}}$ = $\widehat{B_{1}}$.
= $\widehat{A_{4}}$, mà $\widehat{A_{4}}$ = $\widehat{B_{1}}$, từ đó suy ra $\widehat{A_{4}}$ = $\widehat{B_{1}}$.
Xem thêm bài viết khác
- Giải câu 4 trang 31 toán VNEN 7 tập 1
- Giải câu 3 trang 11 toán VNEN 7 tập 1
- Giải câu 2 trang 17 toán VNEN 7 tập 1
- Giải VNEN các môn lớp 7
- Giải câu 1 trang 17 toán VNEN 7 tập 1
- Giải câu 2 trang 48 toán VNEN 7 tập 1
- Giải câu 1 trang 85 toán VNEN 7 tập 1
- Giải câu 1 trang 67 sách toán VNEN lớp 7 tập 1
- Giải câu 4 trang 137 sách toán VNEN lớp 7 tập 1
- Giải câu 2 trang 24 toán VNEN 7 tập 1
- Giải câu 3 trang 137 sách toán VNEN lớp 7 tập 1
- Giải câu 5 trang 77 sách toán VNEN lớp 7 tập 1











