Giải câu 2 bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Câu 2: Trang 43 - sgk giải tích 12
Khảo sát tự biến thiên và vẽ đồ thị của các hàm số bậc bốn sau:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Bài làm:
a)
- Tập xác định: D = R
- Sự biến thiên:
Ta có: ![]()
=> ![]()
- Giới hạn:
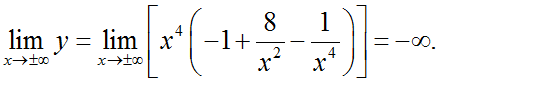
- Bảng biến thiên:
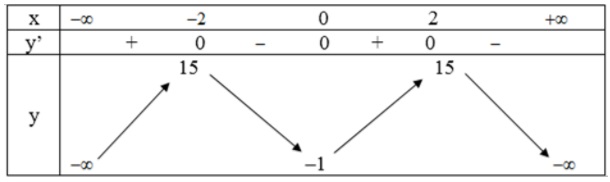
- Hàm số đồng biến trên khoảng (-∞; -2) và (0; 2).
- Hàm số nghịch biến trên các khoảng (-2; 0) và (2; +∞).
- Cực trị: Đồ thị hàm số có điểm cực tiểu là: (0; -1).
Đồ thị hàm số có hai điểm cực đại là: (-2; 15) và (2; 15).
- Đồ thị:
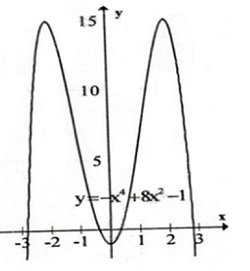
b)
- Tập xác định: D = R
- Sự biến thiên:
Ta có: ![]()
=> ![]()
- Giới hạn:

![]()
- Bảng biến thiên:
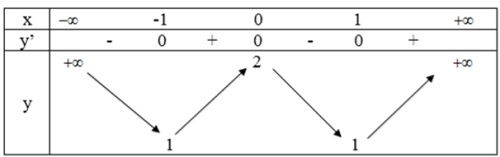
- Hàm số đồng biến trên khoảng (-1; 0) và (1; +∞).
- Hàm số nghịch biến trên các khoảng (-∞; -1) và (0; 1).
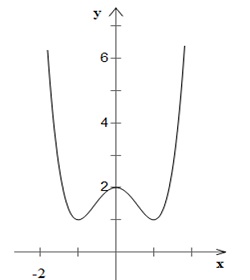
- Cực trị: Đồ thị hàm số có hai điểm cực tiểu là: (-1; 1) và (1; 1).
Đồ thị hàm số có điểm cực đại là: (0; 2).
- Đồ thị:
c)
- Tập xác định: D = R
- Sự biến thiên:
Ta có: ![]()
=> ![]() .
.
- Giới hạn:

![]()
- Bảng biến thiên:
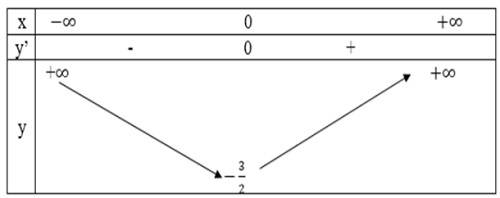
- Hàm số đồng biến trên khoảng (0; +∞).
- Hàm số nghịch biến trên các khoảng (-∞; 0).
- Cực trị: Đồ thị hàm số có điểm cực đại là: (0; -3/2).
- Đồ thị:
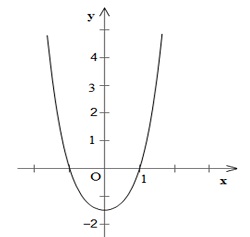
d)
- Tập xác định: D = R
- Sự biến thiên:
Ta có: ![]()
=> ![]() .
.
- Giới hạn:

![]()
- Bảng biến thiên:
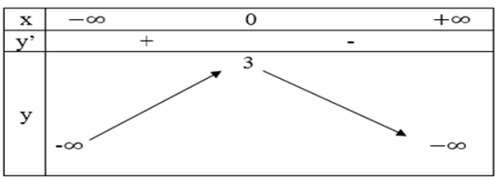
- Hàm số đồng biến trên khoảng (-∞; 0).
- Hàm số nghịch biến trên các khoảng (0; +∞).
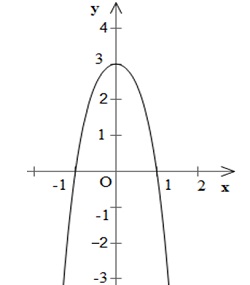
- Cực trị: Đồ thị hàm số có điểm cực đại là: (0; 3).
- Đồ thị:
Xem thêm bài viết khác
- Giải câu 7 bài: Ôn tập chương 2
- Dạng 1: Tìm điều kiện của tham số để hàm phân thức đồng biến trên từng khoảng xác định
- Giải Bài 3: Lôgarit
- Toán 12: Đề kiểm tra học kì 2 dạng trắc nghiệm (Đề 5)
- Giải câu 4 bài: Ôn tập chương 2
- Giải câu 5 bài: Tích phân
- Giải câu 4 bài 1: Sự đồng biến, nghịch biến của hàm số
- Giải câu 2 bài: Lôgarit
- Giải câu 2 bài 2: Cực trị của hàm số
- Giải câu 2 bài: Lũy thừa
- Giải câu 3 bài: Phép chia số phức
- Giải câu 2 bài: Hàm số lũy thừa











