Giải câu 2 trang 104 toán VNEN 9 tập 2

Câu 2: Trang 104 toán VNEN 9 tập 2

a) Cho hai đường tròn có tâm lần lượt là E và F cắt nhau tại hai điểm A và B. AC và AD tương ứng là các đường kính của (E) và (F). Chứng minh rằng AB là đường cao của tam giác ACD.

Hướng dẫn: Xem hình 81

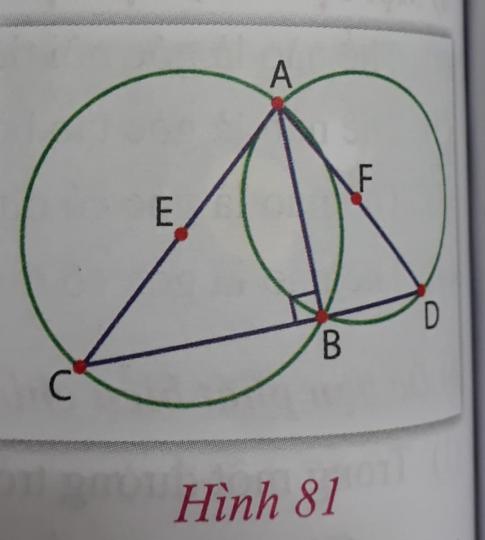
Do AC là đường kính của (E) nên .

Do AD là đường kính của (F) nên .

Từ đó suy ra C, B, D thẳng hàng và

b) Hai đường tròn bằng nhau có tâm tương ứng là I và J cắt nhau tại hai điểm H và G. Đường thẳng d đi qua điểm G cắt (I) tại K và cắt (J) tạo L (K, L khác với điểm G). Chứng minh rằng HK = HL.

Hướng dẫn: Xem hình 82

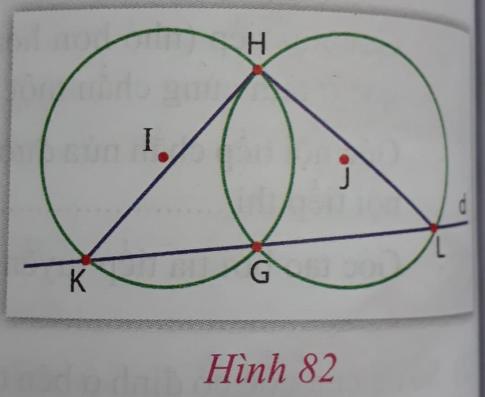
Do hai đường tròn bằng nhau, nên các cung nhỏ HG của (I) và (J) bằng nhau. Suy ra (vì cùng bằng nửa số đo cung nhỏ GH) hay có $......................$

Bài làm:

a) Các em vẽ lại hình 81 vào vở.

Do AC là đường kính của (E) nên .

Do AD là đường kính của (F) nên .

Từ đó suy ra C, B, D thẳng hàng và AB là đường cao của tam giác ACD.

b) Do hai đường tròn bằng nhau, nên các cung nhỏ HG của (I) và (J) bằng nhau. Suy ra (vì cùng bằng nửa số đo cung nhỏ GH) hay có tam giác HKL cân tại H, suy ra HL = HK.