Giải câu 3 trang 85 toán VNEN 9 tập 1

Câu 3: Trang 85 sách VNEN 9 tập 1

Chọn đáp án đúng trong các câu sau

a) Cho < $\alpha$ < ${90}^{\circ }$. Khẳng định nào sau đây là đúng?

A. sin + cos = 1 B. tan = tan (${90}^{\circ }$ - )

C. sin = cos(${90}^{\circ }$ - ) D. cot = cot(${90}^{\circ }$ -)

b) Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 6cm, BC = 7,5cm. Độ dài CH bằng:

A. 4,8cm B. 2,7cm C. 0,6cm D. cm.

c) Cho tam giác ABC vuông tại A, = $\alpha$, AB =1cm, AC = 2cm. Khẳng định nào sau đây là sai?

A. sin = 2cos B.cot = $\frac{1}{2}$

C. = $\frac{1}{3}$ D. $\frac{sin\alpha -2cos\alpha }{sin\alpha +cos\alpha }$ = $\frac{1}{3}$.

Bài làm:

a) Ta có: góc và ${90}^{\circ }$ - là hai góc phụ nhau nên: sin = cos(${90}^{\circ }$ - )

Suy ra đáp án đúng là C.

b)

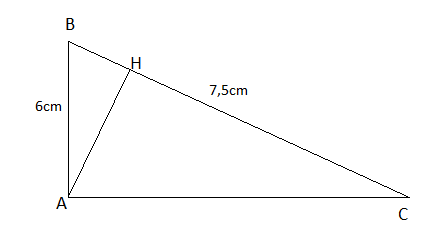
Ta có: AC = = $\sqrt{7,5^2-6^2}$ = 4,5cm

= CH.BC $\Rightarrow$ CH = $\frac{A{C}^2}{BC}$ = 2,7cm

Vậy đáp án B.

c)

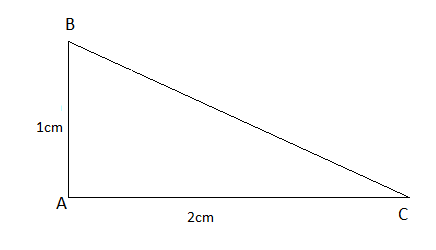
Theo định lý Py-ta-go: BC = = $\sqrt{1^2+2^2}$ = $\sqrt{5}$

*Ta có: cot = $\frac{AB}{AC}$ = $\frac{1}{2}$ suy ra B đúng

* Ta có: sin = $\frac{AC}{BC}$ = $\frac{2}{\sqrt{5}}$

cos = $\frac{AB}{BC}$ = $\frac{1}{\sqrt{5}}$

sin$\alpha$ = 2cos$\alpha$ (1)

Suy ra đáp án A đúng

* Từ (1) suy ra sin - 2cos = 0

$\frac{sin\alpha -2cos\alpha }{sin\alpha +cos\alpha }$ = 0

Suy ra đáp án D sai.

Vậy D sai.