Giải câu 4 trang 56 toán VNEN 9 tập 1

Câu 4: Trang 56 sách VNEN 9 tập 1

Cho hàm số y = mx - 2 (m 0).

a) Với giá trị nào của m thì hàm số đồng biến? Nghịch biến?

b) Xác định giá trị của m để đồ thị hàm số đi qua điểm A(1; 2). Vẽ đồ thị ứng với giá trị m tìm được.

c) Chứng minh rằng với mọi giá trị của m, đồ thị hàm số đã cho đi qua một điểm cố định.

d) Xác định giá trị của m để đồ thị hàm số cắt hai trục tọa độ thành tam giác diện tích bằng 1.

Bài làm:

a) Hàm số y = mx - 2 đồng biến khi m > 0, nghịch biến khi m < 0.

b) Đồ thị hàm số y = mx - 2 đi qua điểm A(1; 2) thì 2 = m.1 - 2 m = 4

Vậy hàm số là y = 4x - 2

Ta có đồ thị như sau:

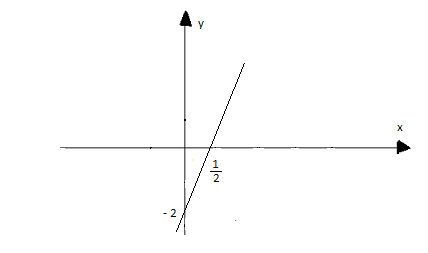
c) Gọi điểm cố định mà hàm số đi qua là M(x0; y0)

Ta có phương trình hoành độ giao điểm là y0 = mx0 - 2 mx0 - (2 + y0) = 0

Vì phương trình có nghiệm với mọi giá trị của m nên

x0 = 0 và 2 + y0 = 0 x0 = 0 và y0 = - 2

Vạy hàm số luôn đi qua điểm cố định M(0; -2).

d) Giả sử hàm số cắt trục hoành, trục tung lần lượt tại A, B

Ta có tọa độ của A, B là A(; 0); (0; -2)

Theo bài ra đồ thị hàm số cắt hai trục tọa độ thành tam giác diện tích bằng 1 hay:

.$\left | \frac{2}{m} \right |$.$\left |- 2 \right |$ = 1

$\left | \frac{2}{m} \right |$ = 1

m = 2 hoặc m = - 2

Vậy m = 2 hoặc m = -2.