Giải câu 4 trang 61 toán VNEN 9 tập 1

Câu 4: Trang 61 sách VNEN 9 tập 1

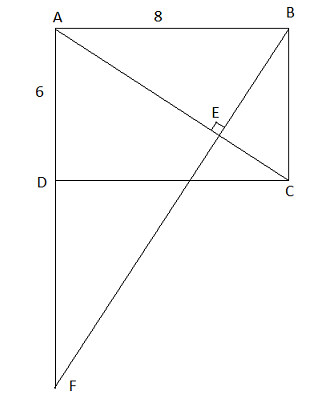
Cho hình chữ nhật ABCD có cạnh BC = 6cm, AB = 8cm. Đường thẳng kẻ từ B vuông góc với AC tại E, cắt cạnh AD tại F.

a) Tính độ dài các đoạn thẳng AC, AE, BE.

b) Tính độ dài các cạnh và diện tích tam giác ABF.

Bài làm:

a) * = $AB^{2}$ + $BC^{2}$ = $6^{2}$ + $8^{2}$ = 100

AC = 10 cm

* Áp dụng công thức = b.a', ta có:

= AE.AC $\Rightarrow $ AE = $\frac{AB^{2}}{AC}$ = $\frac{8^{2}}{10}$ = 6,4 cm.

* Áp dụng định lý Py-ta-go, ta có:

= $AB^{2}$ - $AE^{2}$ = $8^{2}$ - $6,4^{2}$ = 23,04

BE = 4,8 cm.

b) Tam giác ABF có cạnh AB = 8 cm

* Áp dụng công thức = $\frac{1}{b^{2}}$ + $\frac{1}{c^{2}}$, ta có:

= $\frac{1}{AB^{2}}$ + $\frac{1}{AF^{2}}$

$\frac{1}{AF^{2}}$ = $\frac{1}{AE^{2}}$ - $\frac{1}{AB^{2}}$ = $\frac{1}{6,4^{2}}$ - $\frac{1}{8^{2}}$

AF = $\frac{32}{3}$ = 10,7 cm.

* Áp dụng định lý Py-ta-go, ta có:

= $AB^{2}$ + $AF^{2}$ = $8^{2}$ + $(\frac{32}{3})^{2}$

BF = $\frac{40}{3}$ cm

* Diện tích tam giác ABF là

S = .AB.AF = .8.$\frac{32}{3}$ = $\frac{128}{3}$ $cm^{2}$.