Giải câu 5 bài 2: Cực trị của hàm số
Bài 5: Trang 18 - sgk giải tích 12
Tìm a và b để các cực trị của hàm số ![]() đều là những số dương và $x_{0}=-\frac{5}{9}$ là điểm cực đại.
đều là những số dương và $x_{0}=-\frac{5}{9}$ là điểm cực đại.
Bài làm:
TXĐ: ![]()
Nếu a=0 thì y=-9x+b nên hàm số luôn nghịch biến và không có cực trị.
Nếu ![]() ta có $y'=5a^{2}x^{2}+4ax-9=0 \Leftrightarrow \left[ \matrix{x=\frac{1}{a}\hfill \cr x= -\frac{9}{5a}\hfill \cr} \right.$
ta có $y'=5a^{2}x^{2}+4ax-9=0 \Leftrightarrow \left[ \matrix{x=\frac{1}{a}\hfill \cr x= -\frac{9}{5a}\hfill \cr} \right.$
- Với
 ta có bảng biến thiên sau
ta có bảng biến thiên sau
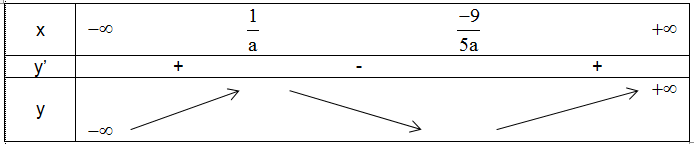
Theo giả thiết ![]() là điểm cực đại nên $\frac{1}{a}=-\frac{5}{9} \Leftrightarrow a=-\frac{9}{5}$
là điểm cực đại nên $\frac{1}{a}=-\frac{5}{9} \Leftrightarrow a=-\frac{9}{5}$
Hơn nữa ![]() .
.
- Với a> 0 ta có bảng biến thiên sau:
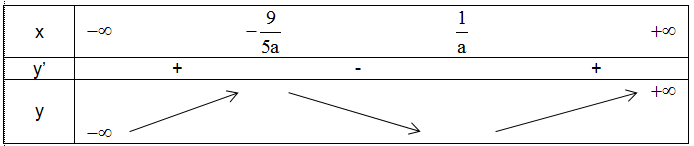
Theo giả thiết ![]() là điểm cực đại nên $-\frac{9}{5a}=-\frac{5}{9}\Leftrightarrow a=\frac{81}{25}$.
là điểm cực đại nên $-\frac{9}{5a}=-\frac{5}{9}\Leftrightarrow a=\frac{81}{25}$.
Hơn nữa ![]()
Vậy giá trị a, b cần tìm là  hoặc $\left\{\begin{matrix}a=\frac{81}{25}\\ b> \frac{400}{243}\end{matrix}\right.$
hoặc $\left\{\begin{matrix}a=\frac{81}{25}\\ b> \frac{400}{243}\end{matrix}\right.$
Xem thêm bài viết khác
- Giải câu 3 bài: Tích phân
- Giải câu 2 bài: Phương trình bậc hai với hệ số thực
- Giải câu 2 bài: Tích phân
- Giải câu 1 bài 1: Sự đồng biến, nghịch biến của hàm số
- Giải câu 8 bài: Ôn tập chương 4
- Dạng 3: Giải bất phương trình mũ và lôgarit bằng phương pháp đưa về cùng cơ số
- Giải câu 6 bài: Ôn tập chương 2
- Giải câu 1 bài: Nguyên hàm
- Giải bài 3: Ứng dụng của tích phân trong hình học
- Giải câu 5 bài 1: Sự đồng biến, nghịch biến của hàm số
- Dạng 3: Xét dấu các hệ số của hàm bậc nhất trên bậc nhất, phân tích đồ thị hàm số.
- Dạng 1: Xét dấu các hệ số của hàm bậc bốn trùng phương, phân tích đồ thị hàm số.











