Giải câu 6 bài 1: Bất đẳng thức sgk Đại số 10 trang 79

Câu 6: trang 79 sgk Đại số 10

Trong mặt phẳng tọa độ Oxy, trên các tia Ox và Oy lần lượt lấy các điểm A và B thay đổi sao cho đường thẳng AB luôn tiếp xúc với đường tròn tâm O bán kính 1. Xác định tọa độ điểm A và B để đoạn AB có độ dài nhỏ nhất.

Bài làm:

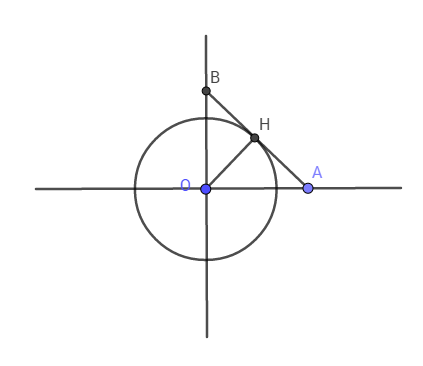
Ta có: (vì \(OH = 1\)).

Vậy diện tích nhỏ nhất khi \(AB\)có độ dài ngắn nhất.

Vì mà \(AH.HB = OH^2= 1\) nên \(AB\) có giá trị nhỏ nhất khi \(AH = HB\)

Hay vuông cân tại

Khi đó (tính chất tam giác cân)

Theo Pi - ta - go ta tính được

Khi đó tọa độ của là và \(B(0; \sqrt2)\).