Trắc nghiệm toán 8 hình học chương 3: Tam giác đồng dạng (P2)

Bài có đáp án. Bộ bài tập trắc nghiệm toán 8 hình học chương 3: Tam giác đồng dạng (P2). Học sinh luyện tập bằng cách chọn đáp án của mình trong từng câu hỏi. Dưới cùng của bài trắc nghiệm, có phần xem kết quả để biết bài làm của mình. Kéo xuống dưới để bắt đầu.

Câu 1: Cho các đoạn thẳng AB = 6cm, CD = 4cm, PQ = 8cm, EF = 10cm, MN = 25mm, RS = 15mm. Hãy chọn phát biểu đúng trong các phát biểu sau?

• A. Đoạn AB và PQ tỉ lệ với hai đoạn thẳng EF vs RS.
• B. Hai đoạn thẳng AB và RS tỉ lệ với hai đoạn thẳng EF và MN.
• C. Hai đoạn thẳng AB và CD tỉ lệ với hai đoạn thẳng PQ và EF
• D. Cả 3 phát biểu đều sai.

Câu 2: Cho tam giác ABC có BC = 8cm; BH và CK (H ∈ AB; K ∈ AC) là hai đường trung tuyến kẻ từ B và C (H ∈ AB; K ∈ AC). Tính độ dài đoạn HK.

• A. HK = 2 cm
• B. HK = 4 cm
• C. HK = 6 cm
• D. HK = 8 cm

Câu 3: Cho ΔABC. Tia phân giác góc trong của góc A cắt BC tại D. Cho AB = 6, AC = x, BD = 9, BC = 21. Tính kết quả đúng của độ dài cạnh x ?

• A. x = 14
• B. x = 12
• C. x = 8
• D. x = 6

Câu 4: Chọn câu trả lời đúng: Cho hình bên, biết DE // AC, tìm x:

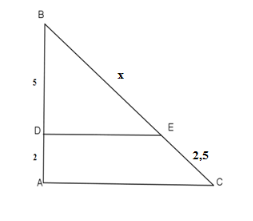
• A. x = 6, 5
• B. x = 6, 25
• C. x = 5
• D. x = 8

Câu 5: Cho tam giác ABC vuông tại A có AB = 6, AC = 8. Tia phân giác góc cắt AC tại D. Độ dài AD là:

• A. 1,5
• B. 3
• C. 4,5
• D. 4

Câu 6: Cho tam giác ABC. Các điểm D, E, F theo thứ tự là trung điểm của BC, CA, AB. Các điểm A′, B′, C′ theo thứ tự là trung điểm của EF, DF, DE. Chọn câu đúng?

• A. ΔA′B′C′ ∽ ΔABC theo tỉ số
• B. ΔEDF ∽ ΔABC theo tỉ số
• C. ΔA′B′C′ ∽ ΔABC theo tỉ số
• D. ΔA′B′C′ ∽ ΔEDF theo tỉ số

Câu 7: Cho tam giác ABC. Một đường thẳng song song song với BC cắt các cạnh AB và AC theo thứ tự tại D và E. Qua E kẻ đường thẳng song song với CD, cắt AB ở F. Biết AB = 16, AF = 9, độ dài AD là:

• A. 10 cm
• B. 15 cm
• C. 12 cm
• D. 14 cm

Câu 8: Hãy chọn câu đúng. Nếu tam giác ABC đồng dạng với tam giác MNP theo tỉ số k thì tam giác MNP đồng dạng với tam giác ABC theo tỉ số:

• A.
• B.
• C.
• D. k

Câu 9: Tam giác có: ABC, , AC = 16 cm, BC = 20 cm. Tính độ dài cạnh AB.

• A. 18 cm
• B. 20 cm
• C. 15 cm
• D. 9 cm

Câu 10: Một người đo chiều cao của cây nhờ 1 cọc chôn xuống đất, cọc cao 2,45 m và đặt xa cây 1,36 m. Sau khi người ấy lùi ra xa cách cọc 0,64 m thì người ấy nhìn thấy đầu cọc và đỉnh cây cùng nằm trên một đường thẳng. Hỏi cây cao bao nhiêu? Biết khoảng cách từ chân đến mắt người ấy là 1,65 m.

• A. 4, 51 m
• B. 5, 14 m
• C. 5, 41 m
• D. 4, 15 m

Câu 11: Cho hình chữ nhật ABCD có E là trung điểm của AB. Tia DE cắt AC ở F, cắt CB ở G. Chọn câu đúng.

• A.
• B. 2FD = FE.FG
• C.
• D. Cả A, B, C đều sai.

Câu 12: Tứ giác ABCD có AB = 8 cm, BC = 15 cm, CD = 18 cm, AD = 10 cm, BD = 12 cm.

Chọn câu đúng nhất:

• A. ΔABD∽ ΔBDC.
• B. ABCD là hình thang.
• C. ABCD là hình thang vuông.
• D. Cả A, B đều đúng.

Câu 13: Cho tam giác ABC có AB = 8cm, AC = 16cm. Điểm D thuộc cạnh AB sao cho BD = 2cm. Điểm E thuộc cạnh AC sao cho CE = 13cm.

Chọn câu đúng.

• A. ΔEDA ∽ ΔABC
• B. ΔADE ∽ ΔABC
• C. ΔAED ∽ ΔABC
• D. ΔDEA ∽ ΔABC

Câu 14: Cho tam giác ABC vuông tại A, gọi H là hình chiếu của A lên BC. Dựng hình bình hành ABCD. Chọn kết luận không đúng:

• A. ΔABC ∽ ΔHCA
• B. ΔADC ∽ ΔCAH
• C. ΔABH ∽ ΔADC
• D. ΔABC = ΔCDA

Câu 15: Hình thang ABCD (AB//CD) có AB = 10cm, CD = 25cm, hai đường chéo cắt nhau tại O.

Chọn khẳng định đúng.

• A. ΔAOB∽ΔCOD với tỉ số đồng dạng k = 2 .
• B.
• C. ΔAOB∽ΔCOD với tỉ số đồng dạng k = .
• D. ΔAOB∽ΔCOD với tỉ số đồng dạng k = .

Câu 16: Cho tam giác ABC có: AB = 9cm, AC = 12cm, BC = 7cm. Chọn kết luận đúng.

• A. \widehat{BAC}$
• B. \widehat{ACB}$
• C. \widehat{ACB}$
• D.

Câu 17: Cho ΔABC có các đường cao BD và CE cắt nhau tại H. Gọi M là giao của AH với BC. Chọn câu đúng.

Chọn khẳng định sai.

• A.
• B.
• C.
• D.

Câu 18: Cho tam giác ABC có AB = 9 cm, điểm D thuộc cạnh AB sao cho AD = 6 cm. Kẻ DE song song với BC (E ∈ AC), kẻ EF song song với CD (F ∈ AB). Tính độ dài AF.

• A. 6 cm
• B. 5 cm
• C. 4 cm
• D. 7 cm

Câu 19: Với giả thiết được cho trong hình, kết quả nào sau đây là đúng ?

• A. y = 10
• B. x = 4, 8
• C. x = 5
• D. y = 8, 25

Câu 20: Cho tam giác ABC vuông tại A, đường cao AH chia cạnh BC thành hai đoạn thẳng HB = 7cm và HC = 18cm. Điểm E thuộc đoạn thẳng HC sao cho đường thẳng đi qua E và vuông góc với BC chia tam giác ABC thành hai phần có diện tích bằng nhau. Tính CE.

• A. 15 cm
• B. 12 cm
• C. 10 cm
• D. 8 cm