[Chân trời sáng tạo] Giải toán 6 bài 3: So sánh phân số

Hướng dẫn giải bài 1: So sánh phân số trang 13 sgk toán 6 tập 2. Đây là sách giáo khoa nằm trong bộ sách "Chân trời sáng tạo" được biên soạn theo chương trình đổi mới của Bộ giáo dục. Hi vọng, với cách hướng dẫn cụ thể và giải chi tiết học sinh sẽ nắm bài học tốt hơn.

1. So sánh hai phân số có cùng mẫu

Hoạt động 1: Trang 13 SGK Chân trời sáng tạo Toán 6 tập 2

Giải:

Công ty A đạt lợi nhuận ít hơn, do < $\frac{-2}{3}$

Thực hành 1: Trang 13 SGK Chân trời sáng tạo Toán 6 tập 2

Giải: \frac{2}{-5}$

2. So sánh hai phân số khác mẫu

Hoạt động 2: Trang 13 SGK Chân trời sáng tạo Toán 6 tập 2

Giải:

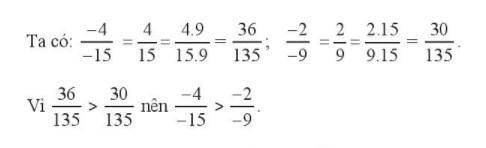
Thực hành 2: Trang 14 SGK Chân trời sáng tạo Toán 6 tập 2

Giải:

Ta có: = $\frac{-7.2}{18.2}$= $\frac{-14}{36}$

= $\frac{-5}{12}$ = $\frac{-5.3}{12.3}$= $\frac{-15}{36}$

Vì > $\frac{-15}{36}$ nên $\frac{-7}{18}$ > $\frac{5}{-12}$

3. Áp dụng quy tắc so sánh hai phân số

Thực hành 3: Trang 14 SGK Chân trời sáng tạo Toán 6 tập 2

Giải:

a) Ta có: 2 = = $\frac{2.15}{1.15}$ = $\frac{30}{15}$ < $\frac{31}{15}$

Suy ra: > $\frac{2}{1}$ hay > 2

b) Ta có: -3 = = $\frac{-3}{1. -2}$ > $\frac{7}{-2}$

Suy ra: > $\frac{7}{-2}$ hay -3 > $\frac{7}{-2}$

Thực hành 4: Trang 14 SGK Chân trời sáng tạo Toán 6 tập 2

Giải:

a) < 0

b) 0 <

c) < $\frac{-5}{-2}$