Đáp án câu 5 đề 3 kiểm tra học kì 2 toán 7

Câu 5: Cho tam giác ABC cân tại A (AB>BC), hai đường cao BD và CE cắt nhau tại H. Chứng minh:

a.

b. AH là đường trung trực của đoạn BC

c. DE và BC song song với nhau

d. AH > CH

Bài làm:

Câu 5:

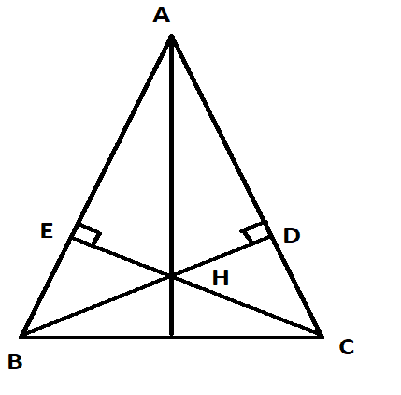
a. Xét và $\bigtriangleup ACE$ có:

AB = AC (gt)

chung

Do đó ( cạnh huyền- góc nhọn)

b. BD và CE là hai đường cao của tam giác ABC (gt) mà BD cắt CE tại H nên H là trực tâm

Mặt khác là tam giác cân tại A (gt) nên đường cao AH cũng đồng thời là đường trung trực của BC

c. Ta có (cmt) => AD=AE

Do đó cân tại A.

Ta có (1)

Tương tự cân tại A có $\widehat{ACB}=\widehat{ABC}=\frac{180^{\circ}-\widehat{A}}{2}$ (2)

Từ (1) và (2) => ED // BC (cặp góc đồng vị bằng nhau)

d. Ta có AB> BC (gt) => AD> CD (quan hệ đường xiên hình chiếu)

=> AH>CH