Giải câu 18 bài: Luyện tập sgk Toán Hình 8 tập 1 Trang 75

Câu 18: Trang 75- sgk toán 8 tập 1

Chứng minh định lý: "Hình thang có hai đường chéo bằng nhau là hình thang cân" qua bài toán sau: Cho hình thang ABCD (AB // CD) có AC = BD. Qua B kẻ đường thẳng song song với AC, cắt đường thẳng DC tại E. Chứng minh rằng :

a) ΔBDE là tam giác cân.

b) ΔACD = ΔBDC.

c) Hình thang ABCD là hình thang cân.

Bài làm:

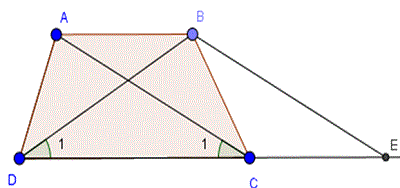
a) Hình thang ABEC (AB//CE) có :AC // BE

=> AC = BE (1)

Theo giả thiết AC = BD (2)

Từ (1), (2) suy ra BE = BD => ΔBDE cân . ( đpcm )

b) Ta có: AC // BE => (3)

Xét cân tại B => $\widehat{D_{1}}=\widehat{E}$

Từ (3), (4) =>

Xét và $\triangle BCD$ có :

• AC = BD ( gt)
• ( cmt )
• CD chung

=> ( c-g-c ) ( đpcm )

c) Từ câu b): và $\triangle BCD$

=>

Vậy Hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân. ( đpcm )