Giải câu 2 bài 5: Dấu của tam thức bậc hai sgk Đại số 10 trang 105

Câu 2: trang 105 sgk Đại số 10

Lập bảng xét dấu các biểu thức sau

a) ;

b) ;

c) ;

d)

Bài làm:

a)

$3x^2-10x+3=0\iff [\begin{array}{c}x=\frac{1}{3}\hfill \\ x=3\hfill \end{array}$

Ta lập bảng xét dấu

Kết luận:

với $x\in \left(-\mathrm{\infty };\frac{1}{3}\right)\cup \left(\frac{5}{4};3\right)$

với $x\in \left(\frac{1}{3};\frac{5}{4}\right)\cup \left(3;+\mathrm{\infty }\right)$

với $x\in \{\frac{1}{3};\frac{5}{4};3\}$

b)

Ta lập bảng xét dấu

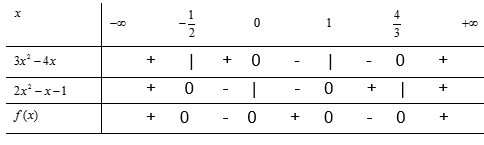
Kết luận:

với $x\in (-\frac{1}{2};0)\cup (1;\frac{4}{3})$

với $x\in (-\mathrm{\infty };-\frac{1}{2})\cup (0;1)\cup (\frac{4}{3};+\mathrm{\infty })$

với $x\in \{-\frac{1}{2};0;1;\frac{4}{3}\}$

c)

Ta lập bảng xét dấu

Kết luận:

với $x\in (-\frac{9}{2};-\frac{1}{2})\cup (\frac{1}{2};+\mathrm{\infty })$

với $x\in (-\mathrm{\infty };-\frac{9}{2})\cup (-\frac{1}{2};\frac{1}{2})$

với $x\in \{-\frac{9}{2};-\frac{1}{2};\frac{1}{2}\}$

d)

Ta lập bảng xét dấu

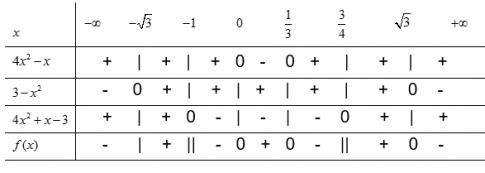
Kết luận:

với $x\in (-\mathrm{\infty };-\sqrt{3})\cup (-1;0)\cup (\frac{1}{3};\frac{3}{4})\cup (\sqrt{3};+\mathrm{\infty })$

với $x\in (-\sqrt{3};-1)\cup (0;\frac{1}{3})\cup (\frac{3}{4};\sqrt{3})$

với $x\in \{-\sqrt{3};0;\frac{1}{3};\sqrt{3}\}$