Giải câu 2 trang 133 sách toán VNEN lớp 7 tập 1

Câu 2: Trang 133 sách toán VNEN lớp 7 tập 1

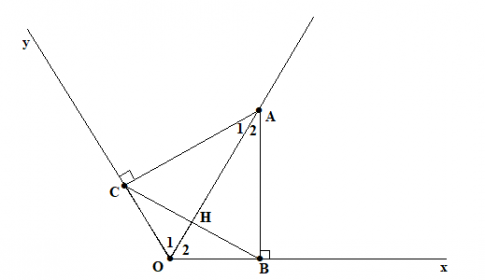
Cho , điểm A thuộc tia phân giác của góc đó. Kẻ AB vuông góc với Ox (B thuộc Ox) , kẻ AC vuông góc với Oy (C thuộc Oy). Chứng minh rằng:

a) ;

b) đều;

c) OA BC.

Bài làm:

a) Xét hai tam giác vuông: và $△OAC$ có:

(OA là tia phân giác);

OA chung;

$△OAB=△OAC$ (c.g.c)

b) Theo câu a) AB = AC và (hai cạnh và hai góc tương ứng).

$△ABC$ là tam giác cân tại A. (1)

OA là tia phân giác của mà $\widehat{xOy}={120}^{\circ }$ nên $\widehat{O_1}=\widehat{O_2}={60}^{\circ }$.

Xét tam giác OAB có .

$\widehat{A_2}={180}^{\circ }-{60}^{\circ }-{90}^{\circ }={30}^{\circ }$

$\widehat{A_1}=\widehat{A_2}={30}^{\circ }$ $\widehat{BAC}=\widehat{A_1}+\widehat{A_2}={60}^{\circ }$. (2)

Từ (1) và (2): Tam giác ABC cân có một góc bằng nên là tam giác đều.

c) Gọi H là giao điểm của OA và BC.

Xét và $△AHC$

AB = AC (hai cạnh tương ứng);

(cmt);

AH chung;

Do đó (c.g.c).

$\widehat{AHB}=\widehat{AHC}$.

Mà hai góc AHB và AHC là hai góc kề bù nên: .

Suy ra: .

Suy ra: AH BC (đpcm) hay OA BC (đpcm).