Giải câu 2 trang 145 sách toán VNEN lớp 7 tập 1

Câu 2: Trang 145 sách toán VNEN lớp 7 tập 1

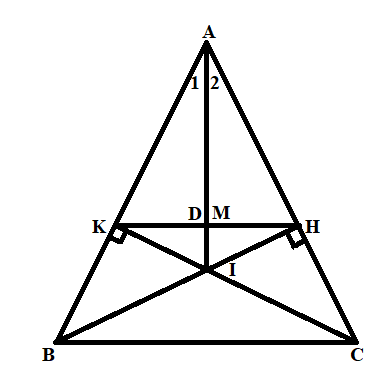
Cho tam giác ABC cân tại A () . Vẽ BH vuông góc với AC (H thuộc AC), CK vuông góc với AB (K thuộc AB).

a) Chứng minh rằng BH = CK.

b) Gọi I là giao điểm của BH và CK. Chứng minh AI là phân giác của góc A.

c) Lấy M là trung điểm của HK. Chứng minh rằng A, M, I thẳng hàng.

Bài làm:

Xét và $△ACK$ vuông tại H và K có:

AB = AC (do cân tại A);

chung;

$△ABH=△ACK$ (cạnh huyền – góc nhọn);

BH = CK (hai cạnh tương ứng).

b) Theo phần a) AH = AK;

Xét và $△AKI$ vuông tại H và K có:

AI chung;

AH = AK (cmt);

$△AHI=△AKI$ (hai cạnh góc vuông);

$\widehat{A_1}=\widehat{A_2}$.

AI là tia phân giác của góc A (đpcm);

c) Gọi giao điểm của AI và KH là D. Ta phải chứng minh: D là trung điểm của HK hay .

Xét và $△AHD$ có

AD chung;

(cmt);

AK = AH (cmt);

$△AKD=△AHD$ (c.g.c)

KD = HD (hai cạnh tương ứng);

Lại có D nằm giữa K và H (theo cách vẽ), nên D là trung điểm của HK.

$D\equiv M$ (A, M, I thẳng hàng).