Giải câu 2 trang 58 sách toán VNEN lớp 8 tập 2
Câu 2: Trang 58 sách VNEN 8 tập 2
Tam giác ABC có độ dài các cạnh AB = a, AC = b và AD là đường phân giác. Chứng minh rằng tỉ số diện tích của tam giác ABD và tam giác ACD bằng ![]() .
.
Bài làm:
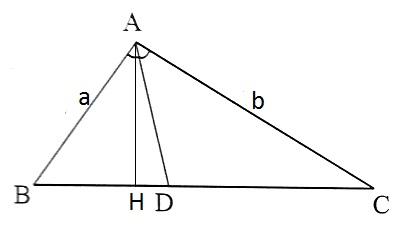
Từ A kẻ AH vuông góc với BC => AH là đường cao của tam giác ABD và tam giác ADC.
![]() = $\frac{\frac{1}{2}.AH.BD}{\frac{1}{2}.AH.DC}$ = $\frac{BD}{DC}$ (1)
= $\frac{\frac{1}{2}.AH.BD}{\frac{1}{2}.AH.DC}$ = $\frac{BD}{DC}$ (1)
Vì AD là đường phân giác của tam giác ABC nên ta có: ![]() = $\frac{AB}{AC}$ = $\frac{a}{b}$ (2)
= $\frac{AB}{AC}$ = $\frac{a}{b}$ (2)
Từ (1), (2) ta có ![]() = $\frac{a}{b}$
= $\frac{a}{b}$
Hay tỉ số diện tích của tam giác ABD và tam giác ACD bằng ![]()
Xem thêm bài viết khác
- Giải câu 3 trang 15 sách toán VNEN lớp 8 tập 2
- Giải toán VNEN 8 bài 6: Ôn tập chương III
- Giải câu 1 trang 28 sách toán VNEN lớp 8 tập 2
- Giải toán VNEN 8 bài 2: Thể tích của hình hộp chữ nhật
- Giải câu 1 trang 71 sách toán VNEN lớp 8 tập 2
- Giải câu 1 trang 24 sách toán VNEN lớp 8 tập 2
- Giải câu 1 trang 58 sách toán VNEN lớp 8 tập 2
- Giải câu 1 trang 63 sách toán VNEN lớp 8 tập 2
- Giải câu 4 trang 24 sách toán VNEN lớp 8 tập 2
- Giải toán VNEN 8 bài 1: Hình hộp chữ nhật
- Giải câu 4 trang 29 sách toán VNEN lớp 8 tập 2
- Giải câu 4 trang 100 sách toán VNEN lớp 8 tập 2











