Giải câu 2 trang 91 toán VNEN 9 tập 1

Câu 2: Trang 91 sách VNEN 9 tập 1

Chứng minh các định lý sau:

a) Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.

b) Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp tam giác đó thì tam giác đó vuông.

Bài làm:

a) Chứng minh: Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.

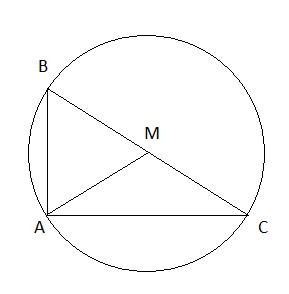
Gọi M là trung điểm của cạnh huyền BC

Theo tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông ta có: MA = MB = MC A, B, C cùng thuộc một đường tròn tâm M hay âm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền (đpcm)

b) Chứng minh: Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp tam giác đó thì tam giác đó vuông

Giả sử tam giác ABC có BC là đường kính của đường tròn ngoại tiếp tam giác

Gọi M là trung điểm của BC suy ra M là tâm của đường tròn

Khi đó MA = MB = MC hay tam giác ABC vuông tại A

Vậy nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp tam giác đó thì tam giác đó vuông (đpcm).