Giải Câu 3 Bài: Bài tập ôn tập chương 3

Câu 3: Trang 121 - SGK Hình học 11

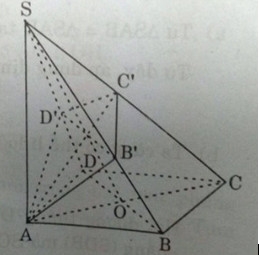
Hình chóp có đáy là hình vuông \(ABCD\) cạnh \(a\), cạnh \(SA\) bằng \(a\) và vuông góc với mặt phẳng \((ABCD)\).

a) Chứng minh rằng các mặt bên của hình chóp là những tam giác vuông.

b) Mặt phẳng đi qua \(A\) và vuông góc với cạnh \(SC\) lần lượt cắt \(SB, SC\) và \(SD\) tại \(B’, C’\) và \(D’\). Chứng minh \(B’D’\) song song với \(BD\) và \(AB’\) vuông góc với \(SB\).

Bài làm:

a)

• Chứng minh vuông

Ta có:

• Chứng minh vuông

Ta có:

• Chứng minh vuông

nên là hình chiếu của \(SB\) trên \(mp(ABCD)\)

là hình vuông nên \(BC ⊥AB\).

Ta có:

\(\left. \matrix{
SA \bot (ABCD) \hfill \cr
BC \bot AB \hfill \cr} \right\}\)

(theo định lí ba đường vuông góc)

là tam giác vuông tại \( B\)

• Chứng minh vuông

nên là hình chiếu của \(SD\) trên \(mp(ABCD)\)

là hình vuông nên \(CD ⊥AD\).

Ta có:

\(\left. \matrix{
SA \bot (ABCD) \hfill \cr
CD \bot AD \hfill \cr} \right\}\)

(theo định lí ba đường vuông góc)

là tam giác vuông tại \( D\)

b)

• Chứng minh

Ta có:

mà

Mặt khác:

Ta có:

=>

• Chứng minh:

Vì (1)

(2)

Từ (1) (2) suy ra