Giải câu 3 trang 140 sách toán VNEN lớp 7 tập 1

Câu 3: Trang 140 sách toán VNEN lớp 7 tập 1

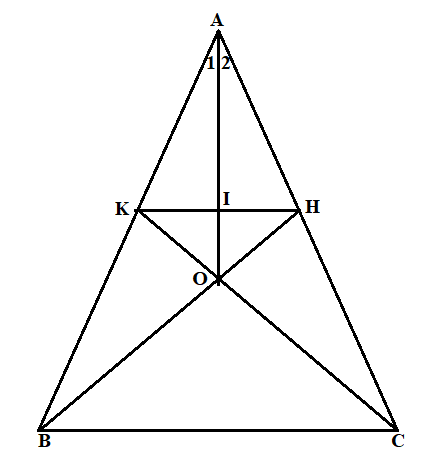
Cho tam giác ABC cân tại A. Lấy điểm H thuộc cạnh AC, điểm K thuộc cạnh AB sao cho AH = AK. Gọi O là giao điểm của BH và CK. Chứng minh rằng:

a) cân;

b) cân;

c) AO đi qua trung điểm KH.

Bài làm:

a) b)

Xét và $△ACK$ có:

Góc A chung;

AH = AK (giả thiết);

AB = AC (giả thiết);

$△ABH=△ACK$ (c.g.c)

Xét và $△HOC$ có:

(hai góc tương ứng của hai tam giác bằng nhau);

BK = CH (hiệu của các đoạn thẳng có độ dài bằng nhau);

(hai góc kề bù với hai góc tương ứng bằng nhau;

$△KOB=△HOC$ (g.c.g);

Suy ra: OB = OC và OK = OH (hai cạnh tương ứng).

Hay tam giác OBC và OKH là những tam giác cân tại O.

c) Xét và $△OAC$ có:

AO chung;

OA = OB (cmt):

AB = AC (giả thiết);

$△OAB=△OAC$ (c.c.c);

$\widehat{A_1}=\widehat{A_2}$.

Gọi I là giao điểm của AO và KH.

Xét và $△HAI$ có:

AI chung;

(cmt);

AK = AH (hiệu của các đoạn thẳng có độ dài bằng nhau);

$△KAI=△HAI$ (c.g.c);

KI = IH hay I là trung điểm của KH

Vậy AO đi qua trung điểm của KH.