Giải câu 34 bài 5: Trường hợp bằng nhau thứ ba của tam giác góc cạnh góc (g.c.g) sgk Toán hình 7 tập 1 Trang 123

Câu 34 : Trang 123 - sgk toán 7 tập 1

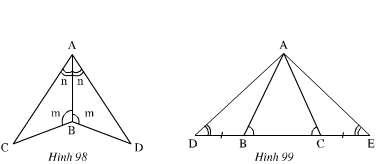
Trên mỗi hình 98, 99 có các tam giác nào bằng nhau ? Vì sao ?

Bài làm:

Hình 98

Xét ∆ABC và ∆ABD có:

= \(\widehat{BAD}\) (gỉa thiết)

AB là cạnh chung

= \(\widehat{ABD}\) (gỉa thiết )

Vậy ∆ABC = ∆ABD (g.c.g)

Hình 99

Ta có : DB = CE => DB + BC = BC + CE

=>DC = BE

Xét ∆ADC và ∆AEB có:

= \(\widehat{E }\) (gt)

= \(\widehat{ABE}\)(gt)

DC = BE (Cmt)

Vậy ∆ADC = ∆AEB (g.c.g)

Ta có:

+ \(\widehat{ABC}\) = 180⁰ (Hai góc kề bù).

+ \(\widehat{ACE}\) = 180⁰ (Hai góc kề bù)

Mặt khác = \(\widehat{ACB}\) (gt)

=> = \(\widehat{ACE}\)

Xét ∆ABD và ∆ACE có:

= \(\widehat{ACE}\) (cmt)

BD = EC (gt)

= \(\widehat{E }\)(gt)

Vậy ∆ABD=∆ACE(g.c.g)