Giải câu 4 trang 85 toán VNEN 9 tập 1

Câu 4: Trang 85 sách VNEN 9 tập 1

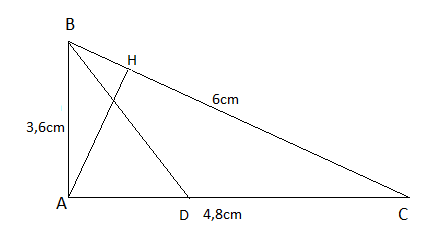
Cho tam giác ABC có AB = 3,6cm, AC = 4,8cm, BC = 6cm.

a) Chứng minh tam giác ABC vuông tại A. Tính các góc B, C và đường cao AH của tam giác đó.

b) Gọi BD là phân giác của góc B. Tính tỉ số diện tích của tam giác ABD và tam giác BDC.

Bài làm:

a)

Ta có: = $\sqrt{3,6^{2} + 4,8^{2}}$ = 6cm = BC

Suy ra tam giác ABC vuông tại A

sinB = = $\frac{4,8}{6}$ $\Rightarrow $ $\widehat{B}$ = $53,13^{\circ}$ $\Rightarrow $ $\widehat{C}$ = $90^{\circ}$ - $53,13^{\circ}$ = $36,87^{\circ}$

Ta có: AH.BC = AB.AC AH = $\frac{AB.AC}{BC}$ = $\frac{3,6.4,8}{6}$ = 2,88cm

b)

SABD = $\frac{1}{2}$.AB.AD

SBDC = $\frac{1}{2}$.AB.DC

$\frac{S\Delta ABD}{S\Delta BDC}$ = $\frac{\frac{1}{2}.AB.AD}{\frac{1}{2}.AB.DC}$ = $\frac{AD}{DC}$

Theo tính chất đường phân giác ta có: = $\frac{AB}{BC}$ = $\frac{3,6}{6}$ = $\frac{3}{5}$

Vậy = $\frac{AD}{DC}$ = $\frac{3}{5}$.