Giải câu 40 bài: Ôn tập chương 3 Hệ hai phương trình bậc nhất hai ẩn sgk Toán đại 9 tập 2 Trang 27

1 Đánh giá

Câu 40: trang 27 sgk toán 9 tập 2

Giải các phương trình sau và minh họa hình học kết quả tìm được :

a. $\left\{\begin{matrix}2x+5y=2 & \\ \frac{2}{5}x+y=1 & \end{matrix}\right.$

b. $\left\{\begin{matrix}0,2x+0,1y=0,3 & \\ 3x+y=5 & \end{matrix}\right.$

c. $\left\{\begin{matrix}\frac{3}{2}x-y=\frac{1}{2} & \\ 3x-2y=1 & \end{matrix}\right.$

Bài làm:

a. $\left\{\begin{matrix}2x+5y=2 & \\ \frac{2}{5}x+y=1 & \end{matrix}\right.$

$\Leftrightarrow \left\{\begin{matrix}2x+5y=2 & \\ 2x+5y=5 & \end{matrix}\right.$

Áp dụng quy tắc cộng đại số, lấy mỗi vế phương trình thứ nhất trừ mỗi vế phương trình thứ hai ta được:

$\left\{\begin{matrix}0x+0y=-3 & \\ 2x+5y=5 & \end{matrix}\right.$

Vậy phương trình vô nghiệm.

Biểu diễn hình học:

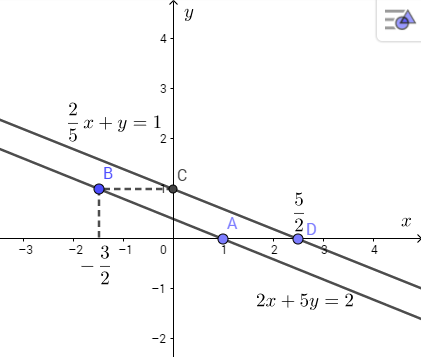
Vẽ đường thẳng 2x + 5y = 2

Cho $y=0\Rightarrow 2x=2\Leftrightarrow x=1$

Ta được điểm $A(1;0)$

Cho $y=1\Rightarrow 2x+5.1=2\Leftrightarrow 2x=-3\Leftrightarrow x=\frac{-3}{2}$

Ta được điểm $B\left ( \frac{-3}{2};1 \right )$

Vẽ đường thẳng đi qua hai điểm A và B vừa xác định, ta được đường thẳng 2x + 5y = 2

Vẽ đường thẳng $\frac{2}{5}x+y=1$

Cho $x=0\Rightarrow y=1$

Ta được điểm $C(0;1)$

Cho $y=0\Rightarrow x=\frac{5}{2}$

Ta được điểm $D\left ( \frac{5}{2};0 \right )$

Vẽ đường thẳng đi qua hai điểm C và D vừa xác định ta được đường thẳng $\frac{2}{5}x+y=1$

b. $\left\{\begin{matrix}0,2x+0,1y=0,3 & \\ 3x+y=5 & \end{matrix}\right.$

$\Leftrightarrow \left\{\begin{matrix}2x+y=3 & \\ 3x+y=5 & \end{matrix}\right.$

Áp dụng quy tắc cộng đại số, lấy mỗi vế phương trình thứ hai trừ mỗi vế phương trình thứ nhất ta được:

$\left\{\begin{matrix}x=2 & \\ 3x+y=5 & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x=2 & \\ 3.2+y=5 & \end{matrix}\right.$

$\Leftrightarrow \left\{\begin{matrix}x=2 & \\ 6+y=5 & \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix}x=2 & \\ y=-1 & \end{matrix}\right.$

Vậy hệ phương trình có một nghiệm duy nhất là $(2;-1)$

Biểu diễn hình học

Vẽ đường thẳng $0,2x+0,1y=0,3$

Cho $x=0\Rightarrow y=3$

Ta được điểm $E(0;3)$

Cho $y=0\Rightarrow x=\frac{3}{2}$

Ta được điểm $F\left ( \frac{3}{2};0 \right )$

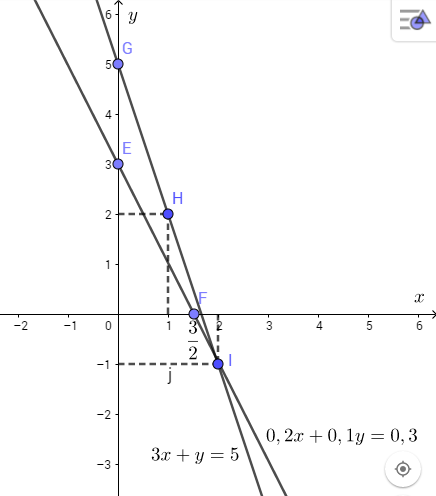
Vẽ đường thẳng đi qua hai điểm E và F vừa xác định ta được đường thẳng $0,2x+0,1y=0,3$

Vẽ đường thẳng 3x + y = 5

Cho $x=0\Rightarrow y=5$

Ta được điểm $G(0;5)$

Cho $x=1\Rightarrow y=2$

Ta được điểm $H(1;2)$

Vẽ đường thẳng đi qua hai điểm G và H ta được đường thẳng 3x + y = 5.

Ta có hai đường thẳng cắt nhau tại điểm $I (2 ; - 1)$

c. $\left\{\begin{matrix}\frac{3}{2}x-y=\frac{1}{2} & \\ 3x-2y=1 & \end{matrix}\right.$

$\Leftrightarrow \left\{\begin{matrix}3x-2y=1 & \\ 3x-2y=1 & \end{matrix}\right.$

Ta có các tỉ số: $\frac{a}{a'}=\frac{b}{b'}=\frac{c}{c'}=1$

Vậy hệ phương trình có vô số nghiệm

Biểu diễn hình học.

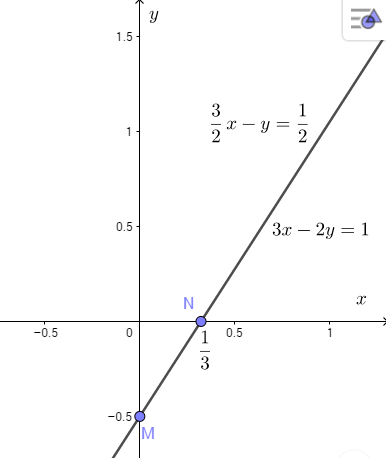
Vẽ đường thẳng $3x-2y=1$

Cho $x=0\Rightarrow y=-\frac{1}{2}$

Ta được điểm $M\left ( 0; -\frac{1}{2} \right )$

Cho $y=0\Rightarrow x=\frac{1}{3}$

Ta được điểm $N\left (\frac{1}{3};0 \right )$

Vẽ đường thẳng đi qua hai điểm M và N vừa xác định ta được đồ thị:

24 lượt xem

Cập nhật: 07/09/2021

Xem thêm bài viết khác

Xem thêm Toán 9 tập 2