Giải câu 42 bài 5: Luyện tập 2 sgk Toán hình 7 tập 1 Trang 124

Câu 42 : Trang 124 - sgk toán 7 tập 1

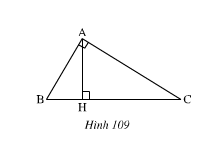
Cho tam giác ABC có = 90⁰, kẻ AH vuông góc với BC(H ∈ BC). C ác tam giác AHC và BAC có AC là cạnh chung, là góc chung, =\(\widehat{BAC}\)=90⁰, nhưng hai tam giác không bằng nhau. Tại sao ở đây không áp dụng trường hợp góc cạnh góc để kết luận ∆AHC = ∆BAC ?

Bài làm:

Xét ∆AHC = ∆BAC có:

AC là cạnh chung

góc chung.

= \(\widehat{BAC}\) = 90⁰

Do góc không phải là góc kề với cạnh AC.

=>∆AHC không bằng ∆BAC.