Giải Câu 43 Bài: Luyện tập sgk Toán 9 tập 2 Trang 83

Câu 43: Trang 83 - SGK Toán 9 tập 2

Cho đường tròn (O) và hai dây cung song song AB, CD (A và C nằm trong cùng một nửa mặt phẳng bờ BD); AD cắt BC tại I. Chứng minh

= $\widehat{AIC}$

Bài làm:

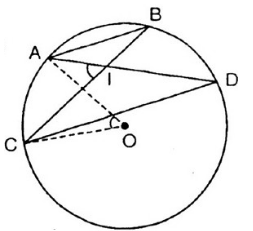
Vì AB // CD (gt) nên cung AC = cung BD (tính chất 2 dây cung song song căng 2 cung bằng nhau). (1)

Ta có: là góc có đỉnh nằm trong (O) => = $\frac{1}{2}$ . (sđ cung AC + sđ cung BD) (2)

Từ (1)(2) suy ra: = sđ cung AC

Mà: sđ cung AC = (góc ở tâm)

=> = $\widehat{AOC}$ (đpcm)