Giải câu 59 Bài: Luyện tập sgk Toán 9 tập 2 Trang 90

Câu 59: Trang 90 - SGK Toán 9 tập 2

Cho hình bình hành ABCD. Đường tròn đi qua ba đỉnh A, B, C cắt đường thẳng CD tại P khác C. Chứng minh AP = AD.

Bài làm:

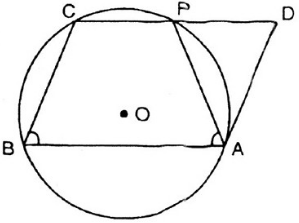
Trong (O), dây cung PC // dây cung AB (do AB // CD) => cung CB = cung AP (2 dây cung // chắn 2 cung bằng nhau)

=> cung CB + cung CP = cung AP + cung CP

=> cung BP = cung AC

=> (2 góc nội tiếp chắn 2 cung bằng nhau)

ABCP có: AB // CP (cmt) => ABCP là hình thang. Lại có: (cmt)

=> ABCP là hình thang cân (dấu hiệu nhận biết)

=> AP = BC (định nghĩa hình thang cân)

Mà BC = AD (2 cạnh đối diện của hình bình hành ABCD)

=> AP = AD (= BC)