Giải Câu 62 Bài 9: Tính chất ba đường cao của tam giác sgk Toán 7 tập 2 Trang 83

Câu 62: Trang 83 - SGK Toán 7 tập 2

Chứng minh rằng một tam giác có hai đường cao (xuất phát từ các đỉnh của hai góc nhọn) bằng nhau thì tam giác đó là tam giác cân. Từ đó suy ra một tam giác có ba đường cao bằng nhau thì tam giác đó là tam giác đều.

Bài làm:

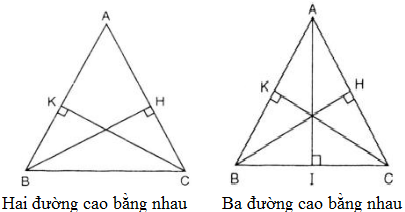
Hai đường cao bằng nhau

Vẽ và $CK ⊥ AB$

Xét hai tam giác vuông KBC và HCB có:

Cạnh BC chung

Xét tam giác ABC, có:

hay $\widehat{ABC}=\widehat{ACB}$

Vậy tam giác ABC cân tại A (đpcm)

Ba đường cao bằng nhau

Từ a) ta có:

Nếu BH = CK thì ΔABC cân tại A => AB = AC (1)

Nếu AI = BH thì ΔABC cân tại C => CA = CB (2)

Từ (1) và (2) ta có: AB = BC = AC

Vậy ΔABC là tam giác đều.