Giải câu 75 bài 11: Hình thoi sgk Toán hình 8 tập 1 Trang 106

Câu 75 : Trang 106 sgk toán 8 tập 1

Chứng minh rằng các trung điểm của bốn cạnh của một hình chữ nhật là các đỉnh của hình thoi.

Bài làm:

Theo giả thiết ta có hình vẽ

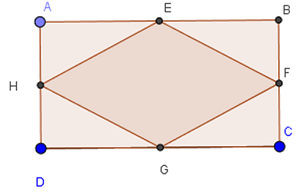
Giả sử hình chữ nhật ABCD có E, F, G. H lần lượt là trung điểm của AB, BC, CD, DA

=>AE = BE = DG = CG = AB = CD

HA = FB = DH = CF = AD = BC

Xét 4 tam giác vuông EAH, EBF, GDH, GCF có:

AE = BE = DG = CG (cmt)

HA = FB = DH = CF (cmt)

=> ∆EAH = ∆EBF = ∆GDH = ∆GCF (c.g.c)

=> EH = EF = GH = GF

Vậy EFGH là hình thoi. (đpcm)