Dạng 2: Xét dấu các hệ số của hàm bậc ba, phân tích đồ thị hàm số.

Dạng 2: Xét dấu các hệ số của hàm bậc ba, phân tích đồ thị hàm số.

Bài làm:

I.Phương pháp giải

Xét đồ thị hàm số .

a) Xác định dấu của a

Từ đồ thị, ta tìm được giới hạn .Ta thấy:

.

.

b) Xác định dấu của d

Ta có M(0; d) là giao điểm của đồ thị hàm số với trục tung. Ta có:

• M nằm phía trên trục hoành .
• M nằm phía dưới trục hoành .
• M nằm trên trục hoành .

c) Xác định dấu của b và c

Gọi lần lượt các điểm cực đại và cực tiểu của hàm số là và $x_{CT}$. Vì và $x_{CT}$ là nghiệm của phương trình $y^{{}^{\prime }}=3a{x}^2+2bx+c=0$ nên $\{\begin{array}{c}{x}_{CD}+x_{CT}=\frac{-2b}{3a}\\ x_{CD}.x_{CT}=\frac{c}{3a}\end{array}$

Xác định dấu của hay dấu của $\frac{c}{a}$ từ đó tìm được dấu của c.

• Nếu các điểm cực trị của đồ thị nằm về cùng một phía với trục tung thì > 0.
• Nếu các điểm cực trị của đồ thị nằm về hai phía với trục tung thì < 0.
• Nếu một trong hai điểm cực trị thuộc trục tung thì = 0.

Xác định dấu của hay dấu của $\frac{-b}{a}$ từ đó tìm được dấu của b.

• Nếu các điểm cực trị của đồ thị nằm bên phải trục tung hoặc thuộc trục tung thì ;
• Nếu các điểm cực trị của đồ thị nằm bên trái trục tung hoặc thuộc trục tung thì ;
• Xét trường hợp hai điểm cực trị của đồ thị nằm về hai phía trục tung. Khi đó, nếu điểm cực trị có hoành độ âm gần trục tung hơn thì , nếu điểm cực trị có hoành độ dương gần trục tung hơn thì $x_{CD}+x_{CT}<0$, nếu hai điểm cực trị cách đều trục tung thì $x_{CD} + x_{CT} = 0.

II.Bài tập vận dụng

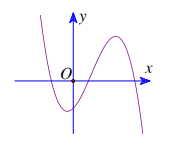
Bài tập 1: Hàm số có đồ thị như hình bên. Xác định dấu của a, b, c, d.

Bài giải:

Ta thấy: do đó a < 0.

Giao điểm của đồ thị hàm số với trục tung là điểm nằm trê trục hoành nên d < 0.

Gọi lần lượt các điểm cực đại và cực tiểu của hàm số là và $x_{CT}$. Vì và $x_{CT}$ là nghiệm của phương trình $y^{{}^{\prime }}=3a{x}^2+2bx+c=0$ nên $\{\begin{array}{c}{x}_{CD}+x_{CT}=\frac{-2b}{3a}\\ x_{CD}.x_{CT}=\frac{c}{3a}\end{array}$

Vì các điểm cực đại, cực tiểu của hàm số nằm về hai phía của Oy nên < 0 do đó a và c trái dấu, nên c > 0.

Vì trong hai điểm cực trị, điểm có hoành độ âm gần trục tung hơn nên > 0. Do đó a, b trái dấu, nên b > 0.

Vậy a < 0; b > 0; c > 0; d < 0.

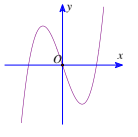
Bài tập 2: Hàm số có đồ thị như hình bên. Xác định dấu của a, b, c, d.

Bài giải:

Ta thấy: do đó a >0.

Giao điểm của đồ thị hàm số với trục tung là điểm nằm trên trục hoành nên d = 0.

Gọi lần lượt các điểm cực đại và cực tiểu của hàm số là và $x_{CT}$. Vì và $x_{CT}$ là nghiệm của phương trình $y^{{}^{\prime }}=3a{x}^2+2bx+c=0$ nên $\{\begin{array}{c}{x}_{CD}+x_{CT}=\frac{-2b}{3a}\\ x_{CD}.x_{CT}=\frac{c}{3a}\end{array}$

Vì các điểm cực đại, cực tiểu của hàm số nằm về hai phía của Oy nên < 0 do đó a và c trái dấu, nên c > 0.

Vì hai điểm cưcj trị cách đều trục tung nên = 0. Do đó b = 0.

Vậy a > 0; b = 0; c < 0; d = 0.