Giải câu 7 bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số

Câu 7: Trang 44 - sgk giải tích 12

Cho hàm số :

a) Với giá trị nào của tham số m, đồ thị của hàm đi qua điểm (-1; 1) ?

b) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số khi .

c) Viết phương trình tiếp tuyến (C) tại điểm có tung độ bằng .

Bài làm:

a) Đồ thị hàm số qua điểm (-1; 1) khi và chỉ khi:

<=> .

Vậy thì đồ thị của hàm đi qua điểm (-1; 1).

b) Với m = 1, ta có:

• TXĐ: D = R
• Sự biến thiên:

Ta có:

=>

• Giới hạn:
• Bảng biến thiên:

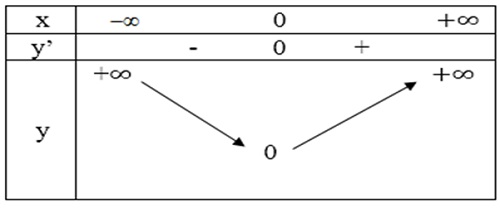
• Hàm số đồng biến trên (0; +∞) và nghịch biến trên (-∞; 0)
• Cực trị: Hàm số có điểm cực tiểu là (0; 1).
• Đồ thị:

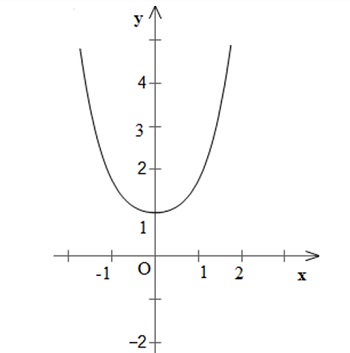
c) Điểm thuộc (C) có tung độ bằng

=> Hoành độ của điểm đó là nghiệm của phương trình:

Đặt

<=>

<=>

<=>

<=>

=> Ta có hai điểm là : và $C(-11;\frac{7}{4})$

Vậy :

• Phương trình tiếp tuyến của (C) tại điểm B là:
• Phương trình tiếp tuyến của (C) tại điểm C là: