Giải câu 2 bài 1: Giá trị lượng giác của một góc bất kì

Câu 2: Trang 40 - sgk hình học 10

Cho AOB là tam giác cân tại O có OA = a và có các đường cao OH và AK. Giả sử.

Tính AK và OK theo a và .

Bài làm:

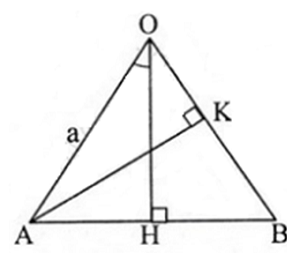
Ta có: OH là đường cao của tam giác cân AOB

=> OH là tia phân giác của

=> .

Xét vuông tại K, ta có: $\frac{AK}{AO}=\sin 2\alpha => AK=a\sin 2\alpha $

Tương tự: