Giải Câu 2 Bài: Ôn tập cuối năm Phần Hình học sgk Toán 8 tập 2 Trang 131

Câu 2: Trang 131 - SGK Toán 8 tập 2

Cho hình thang ABCD (AB // CD) có hai đường chéo cắt nhau ở O và tam giác ABO là tam giác đều. Gọi E, F, G theo thứ tự là trung điểm của các đoạn thẳng OA, OD và BC. Chứng minh rằng tam giác EFG là tam giác đều.

Bài làm:

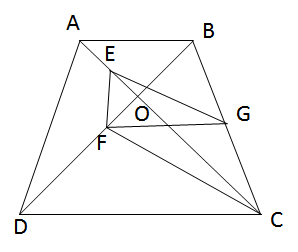
Tam giác ABO đều nên tam giác CDO cũng đều, suy ra OD = OC.

∆AOD = ∆BOC (c.g.c) =>AD = BC.

EF là đường trung bình của tam giác AOD nên:

(1) (1)

CF là đường trung tuyến của tam giác đều CDO nên CF ⊥ DO, nghĩa là .Trong tam giác vuông CFB, FG là đường trung tuyến ứng với cạnh huyền nên:

(2)

Chứng minh tương tự ta cũng có:

(3)

Từ (1), (2), (3) suy ra EF = GF = EG nên tam giác EFG là tam giác đều.