Giải câu 30 bài: Luyện tập sgk Toán hình 9 tập 1 Trang 116

Câu 30: Trang 116 - sgk Toán 9 tập 1

Cho nửa đường tròn tâm O có đường kính AB (đường kính của một đường tròn chia đường tròn đó thành hai nửa đường tròn). Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn, nó cắt Ax và By theo thứ tự ở C và D.

Chứng minh rằng :

a. .

b. CD = AC + BD .

c. Tích AC.BD không đổi khi điểm M di chuyển trên nửa đường tròn.

Bài làm:

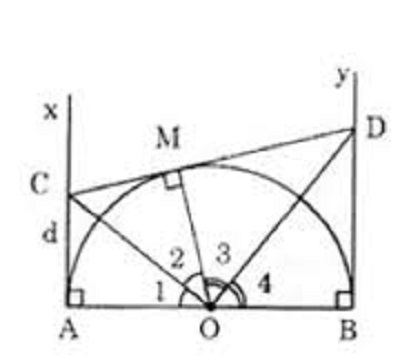a. Theo tính chất của hai tiếp tuyến cắt nhau ta có:

• OC là tia phân giác của
• OD và tia phân giác của

=> OC và OD là các tia phân giác của hai góc kề bù và $\widehat{BOM}$ nên $OC\perp OD$ .

=> ( đpcm ).

b. Theo tính chất của hai tiếp tuyến cắt nhau ta có :

• CM = AC
• DM = BC

=> CD = CM + DM = AC + BD (đpcm).

c. Ta có:

• AC = CM
• BD = DM

=> AC.BD = CM.MD .

Xét vuông tại O, ta có :

(R là bán kính đường tròn O).

<=>

Mà R không đổi => AC.BD không đổi .

Vậy Tích AC.BD không đổi khi điểm M di chuyển trên nửa đường tròn.