Giải câu 31 Bài: Luyện tập sgk Toán 9 tập 2 Trang 79

Câu 31: Trang 79 – SGK Toán 9 tập 2

Cho đường tròn (O; R) và dây cung BC = R . Hai tiếp tuyến của đường tròn (O) tại B, C cắt nhau ở A. Tính và $\widehat{BAC}$

Bài làm:

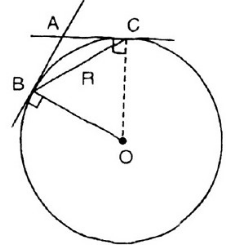
Tam giác OBC đều (do OB = OC = OA =R) => = $60^{\circ}$

Mặt khác: là góc nội tiếp chắn cung BC của (O)

=> = số đo cung BC (định lý về góc nội tiếp chắn cung)

=> số đo cung BC =

Ta có: là góc tạo bởi tia tiếp tuyến BA và dây cung BC

suy ra = $\frac{1}{2}$ số đo cung BC = $30^{\circ}$ (định lý về góc tạo bởi tia tiếp tuyến và dây cung)

Trong tam giác ABC có: = $180^{\circ}$ - $\widehat{BOC}$ = $180^{\circ}$ - $60^{\circ}$ = $120^{\circ}$