Giải Câu 5 Bài 3: Phương trình đường elip sgk Hình học 10 Trang 88

Câu 5: Trang 88 - SGK Hình học 10

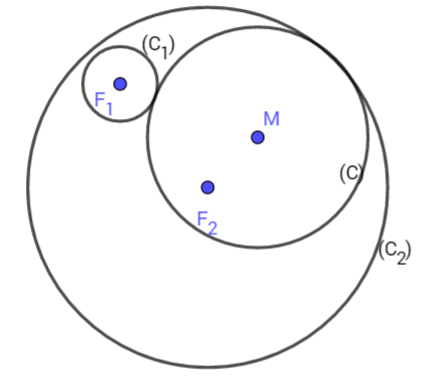
Cho hai đường tròn và $C_2(F_2;R_2)$. $C_1$ nằm trong $C_2$ và $F_1\ne F_2$. Đường tròn $(C)$ thay đổi luôn tiếp xúc ngoài với $C_1$ và tiếp xúc trong với $C_2$.Hãy chứng tỏ rằng tâm $M$ của đường tròn $(C)$ di động trên một elip.

Bài làm:

Gọi là bán kính của đường tròn $(C)$.

Vì và $C_1$ tiếp xúc ngoài với nhau, cho ta:

(1)

Vì và $C_2$ tiếp xúc trong với nhau, cho ta:

(2)

Từ (1) VÀ (2) ta được:

không đổi.

Điểm M có tổng các khoảng cách đến hai điểm cố định $F_1$ và $F_2$ bằng một độ dài không đổi $R_1+R_2$.

Vậy tập hợp điểm là đường elip, có các tiêu điểm $F_1$ và $F_2$ và có tiêu cự $F_1{F}_2=R_1+R_2$.