Giải Câu 7 Bài: Ôn tập cuối năm sgk Hình học 10 Trang 99

Câu 7: Trang 99 - SGK Hình học 10

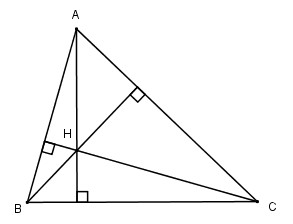
Cho tam giác với $H$ là trực tâm. Biết phương trình của đường thẳng $AB,BH$ và $AH$ lần lượt là: $4x+y–12=0,5x–4y–15=0$ và $2x+2y–9=0$

Hãy viết phương trình hai đường thẳng chứa hai cạnh còn lại và đường cao thứ ba.

Bài làm:

• Ta có: là giao của hai đường thẳng $AB;AH$ nên tọa độ đỉnh là nghiệm của hệ:

$\{\begin{array}{c}4x+y-12=0\hfill \\ 2x+2y-9=0\hfill \end{array}$

Giải hệ ta được:

Đường thẳng có vecto chỉ phương $\overrightarrow{u}=(4;5)$

Cạnh vuông góc với $BH$ nên nhận vecto u làm một vecto pháp tuyến, đi qua $A(\frac{5}{2};2)$.

Phương trình có vecto pháp tuyến , đi qua $A(\frac{5}{2};2)$ là:

• Tương tự, là giao của hai đường thẳng $AB;BH$ nên tọa độ đỉnh là nghiệm của hệ:

$\{\begin{array}{c}4x+y-12=0\hfill \\ 6x-4y-15=0\hfill \end{array}$

Giải hệ ta được:

Ta có: có vecto chỉ phương $\overrightarrow{v}=(-2;2)=2(-1;1)$.

Vì: vuông góc với $AH$ nên nhận vecto làm vecto pháp tuyến.

Phương trình có vecto pháp tuyến $\overrightarrow{v^{\prime }}=(-1;1)$ và đi qua điểm là:

• Ta có: là giao điểm của hai đường thẳng $AH,BH$ nên tọa độ là nghiệm của hệ phương trình:

$\{\begin{array}{c}5x-4y-15=0\hfill \\ 2x+2y-9=0\hfill \end{array}$

Giải hệ ta được:

Đường cao đi qua $H$ và vuông góc với $AB$

Hoàn toàn tương tự, ta viết được phương trình của :