Giải câu 9 trang 140 sách toán VNEN lớp 7 tập 1

Câu 9: Trang 140 sách toán VNEN lớp 7 tập 1

Cho tam giác đều ABC. Lấy các điểm D, E, F theo thứ tự thuộc các cạnh AB, BC, CA sao cho AD = BE = CF. Chứng minh rằng là tam giác đều.

Bài làm:

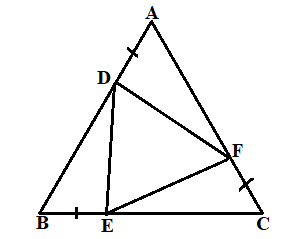
Dễ thấy (c.g.c) do có: $\widehat{A} = \widehat{B} = \widehat{C} = 60^{\circ}$; AD = BE = CF (giả thiết); AF = BD = CE (hiệu của những đoạn thẳng có cùng độ dài).

DE = EF = DF $\bigtriangleup DEF$ là tam giác đều (đpcm).