Giải toán VNEN 8 bài 5: Trường hợp đồng dạng thứ nhất
Giải bài 5: Trường hợp đồng dạng thứ nhất - Sách VNEN toán 8 tập 2 trang 64. Phần dưới sẽ hướng dẫn trả lời và giải đáp các câu hỏi trong bài học. Cách làm chi tiết, dễ hiểu, Hi vọng các em học sinh nắm tốt kiến thức bài học.
A.B. HOẠT ĐỘNG KHỞI ĐỘNG và HÌNH THÀNH KIẾN THỨC
1. a) Cho ![]() ABC và
ABC và ![]() A'B'C' có các kích thước như hình 30 (cùng đơn vị đo là cen-ti-met). Hỏi
A'B'C' có các kích thước như hình 30 (cùng đơn vị đo là cen-ti-met). Hỏi ![]() ABC và
ABC và ![]() A'B'C' có đồng dạng với nhau không?
A'B'C' có đồng dạng với nhau không?

Điền vào chỗ trống (...) để hoàn thiện lời giải:
- Lấy M trên AB sao cho AM = 1,5cm.Qua M kẻ đường thẳng song song với BC cắt cạnh AC tại N.
- Vì MN // BC nên ![]() AMN $\sim $
AMN $\sim $ ![]() ......
......
Suy ra ![]() = $\frac{AN}{AC}$ = $\frac{MN}{BC}$, hay $\frac{1,5}{3}$ = $\frac{AN}{4}$ = $\frac{MN}{6}$ nên AN = $\frac{4 . 1,5}{3}$ = 2 (cm) và MN = $\frac{6 . 1,5}{3}$ = 3 (cm).
= $\frac{AN}{AC}$ = $\frac{MN}{BC}$, hay $\frac{1,5}{3}$ = $\frac{AN}{4}$ = $\frac{MN}{6}$ nên AN = $\frac{4 . 1,5}{3}$ = 2 (cm) và MN = $\frac{6 . 1,5}{3}$ = 3 (cm).
Vậy ![]() AMN =
AMN = ![]() ........(AM = A'B'; AN =.........; MN = .........).
........(AM = A'B'; AN =.........; MN = .........).
Suy ra ![]() AMN $\sim $ .........
AMN $\sim $ .........
Từ (1) và (2) suy ra ![]() ABC $\sim $
ABC $\sim $ ![]() A'B'C'.
A'B'C'.
Trả lời:
- Lấy M trên AB sao cho AM = 1,5cm.Qua M kẻ đường thẳng song song với BC cắt cạnh AC tại N.
- Vì MN // BC nên ![]() AMN $\sim $
AMN $\sim $ ![]() ABC
ABC
Suy ra ![]() = $\frac{AN}{AC}$ = $\frac{MN}{BC}$, hay $\frac{1,5}{3}$ = $\frac{AN}{4}$ = $\frac{MN}{6}$ nên AN = $\frac{4 . 1,5}{3}$ = 2 (cm) và MN = $\frac{6 . 1,5}{3}$ = 3 (cm).
= $\frac{AN}{AC}$ = $\frac{MN}{BC}$, hay $\frac{1,5}{3}$ = $\frac{AN}{4}$ = $\frac{MN}{6}$ nên AN = $\frac{4 . 1,5}{3}$ = 2 (cm) và MN = $\frac{6 . 1,5}{3}$ = 3 (cm).
Vậy ![]() AMN =
AMN = ![]() A'B'C' (AM = A'B'; AN = A'C'; MN = B'C').
A'B'C' (AM = A'B'; AN = A'C'; MN = B'C').
Suy ra ![]() AMN $\sim $ A'B'C'
AMN $\sim $ A'B'C'
Từ (1) và (2) suy ra ![]() ABC $\sim $
ABC $\sim $ ![]() A'B'C'.
A'B'C'.
2. a) Cho hình 32, độ dài các cạnh cho trên hình vẽ ( có cùng đơn vị đo cen-ti-met).
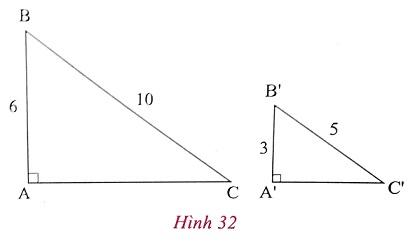
* Tính AC và A'C'.
* Chứng tỏ ![]() A'B'C' $\sim $
A'B'C' $\sim $ ![]() ABC.
ABC.
Điền vào chỗ trống (...) để hoàn thiện lời giải
* Áp dụng định lí Py-ta-go vào ![]() A'B'C' vuông tại A', có:
A'B'C' vuông tại A', có:
![]() + $A'C'^{2}$ = $B'C'^{2}$ hay $A'C'^{2}$ = ...........suy ra A'C' = $\sqrt{16}$ = ........(cm).
+ $A'C'^{2}$ = $B'C'^{2}$ hay $A'C'^{2}$ = ...........suy ra A'C' = $\sqrt{16}$ = ........(cm).
Áp dụng định lí Py-ta-go vào ![]() ABC vuông tại A, có:
ABC vuông tại A, có:
![]() + $AC^{2}$ = $BC^{2}$ hay $AC^{2}$ = ...........suy ra AC =............ = 8 (cm).
+ $AC^{2}$ = $BC^{2}$ hay $AC^{2}$ = ...........suy ra AC =............ = 8 (cm).
* ![]() A'B'C' và
A'B'C' và ![]() ABC, có: $\frac{A'B'}{AB}$ = $\frac{......}{AC}$ = $\frac{B'C'}{.......}$ (Vì $\frac{3}{6}$ = $\frac{4}{8}$ = $\frac{5}{10}$ = $\frac{1}{2}$).
ABC, có: $\frac{A'B'}{AB}$ = $\frac{......}{AC}$ = $\frac{B'C'}{.......}$ (Vì $\frac{3}{6}$ = $\frac{4}{8}$ = $\frac{5}{10}$ = $\frac{1}{2}$).
Vậy ![]() ABC $\sim $
ABC $\sim $ ![]() .........
.........
Trả lời:
* Áp dụng định lí Py-ta-go vào ![]() A'B'C' vuông tại A', có:
A'B'C' vuông tại A', có:
![]() + $A'C'^{2}$ = $B'C'^{2}$ hay $A'C'^{2}$ = 16 suy ra A'C' = $\sqrt{16}$ = 4(cm).
+ $A'C'^{2}$ = $B'C'^{2}$ hay $A'C'^{2}$ = 16 suy ra A'C' = $\sqrt{16}$ = 4(cm).
Áp dụng định lí Py-ta-go vào ![]() ABC vuông tại A, có:
ABC vuông tại A, có:
![]() + $AC^{2}$ = $BC^{2}$ hay $AC^{2}$ = 64 suy ra AC = $\sqrt{64}$ = 8 (cm).
+ $AC^{2}$ = $BC^{2}$ hay $AC^{2}$ = 64 suy ra AC = $\sqrt{64}$ = 8 (cm).
* ![]() A'B'C' và
A'B'C' và ![]() ABC, có: $\frac{A'B'}{AB}$ = $\frac{A'C'}{AC}$ = $\frac{B'C'}{BC}$ (Vì $\frac{3}{6}$ = $\frac{4}{8}$ = $\frac{5}{10}$ = $\frac{1}{2}$).
ABC, có: $\frac{A'B'}{AB}$ = $\frac{A'C'}{AC}$ = $\frac{B'C'}{BC}$ (Vì $\frac{3}{6}$ = $\frac{4}{8}$ = $\frac{5}{10}$ = $\frac{1}{2}$).
Vậy ![]() ABC $\sim $
ABC $\sim $ ![]() A'B'C'.
A'B'C'.
d) Tìm trong hình 34 các cặp tam giác đồng dạng:
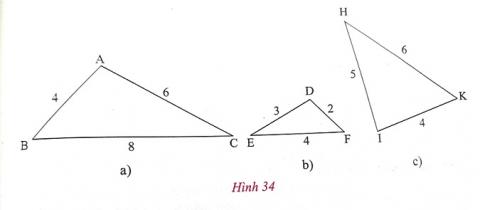
Trả lời:
Ta có: ![]() = $\frac{4}{2}$ = 2
= $\frac{4}{2}$ = 2
![]() = $\frac{6}{3}$ = 2
= $\frac{6}{3}$ = 2
![]() = $\frac{8}{4}$ = 2
= $\frac{8}{4}$ = 2
![]() $\frac{AB}{DF}$ = $\frac{AC}{DE}$ = $\frac{BC}{EF}$ = 2
$\frac{AB}{DF}$ = $\frac{AC}{DE}$ = $\frac{BC}{EF}$ = 2
![]() $\Delta $ ABC $\sim $ $\Delta $ DFE.
$\Delta $ ABC $\sim $ $\Delta $ DFE.
B. BÀI TẬP VÀ HƯỚNG DẪN GIẢI
Kiến thức thú vị
C. HOẠT ĐỘNG LUYỆN TẬP
Câu 1: Trang 67 sách VNEN 8 tập 2
Cho hai tam giác ABC và A'B'C' có kích thước như trong hình 35.

a) ![]() ABC và
ABC và ![]() A'B'C' có đồng dạng vói nhau không? Vì sao?
A'B'C' có đồng dạng vói nhau không? Vì sao?
b) Tính tỉ số chu vi của hai tam giác đó.
Câu 2: Trang 68 sách VNEN 8 tập 2
Tam giác ABC có độ dài các cạnh là AB = 3cm, AC = 4cm, BC = 8cm. Tam giác A'B'C' đồng dạng với tam giác ABC và có chu vi bằng 45cm. Hãy tính độ dài các cạnh của tam giác A'B'C'.
Câu 3: Trang 68 sách VNEN 8 tập 2
Cho hai tam giác đồng dạng có tỉ số chu vi là ![]() và hiệu độ dài hai cạnh tương ứng của chúng là 14,6 cm. Tính độ dài hai cạnh đó.
và hiệu độ dài hai cạnh tương ứng của chúng là 14,6 cm. Tính độ dài hai cạnh đó.
D. HOẠT ĐỘNG VẬN DỤNG và TÌM TÒI, MỞ RỘNG
Câu 1: Trang 68 sách VNEN 8 tập 2
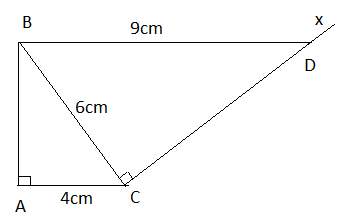
Cho tam giác ABC vuông tại A, AC = 4cm; BC = 6cm. Kẻ tia Cx vuông góc với BC (tia Cx và điểm A nằm khác phía với đường thẳng BC). Lấy trên Cx điểm D sao cho BD = 9cm (h,36). Chứng minh BD // AC.
Xem thêm bài viết khác
- Giải câu 6 trang 17 sách toán VNEN lớp 8 tập 2
- Giải câu 2 trang 97 sách toán VNEN lớp 8 tập 2
- Giải câu 3 trang 101 sách toán VNEN lớp 8 tập 2
- Giải câu 6 trang 24 sách toán VNEN lớp 8 tập 2
- Giải câu 4 trang 100 sách toán VNEN lớp 8 tập 2
- Giải câu 2 trang 46 sách toán VNEN lớp 8 tập 2
- Giải câu 1 trang 17 sách toán VNEN lớp 8 tập 2
- Giải câu 1 trang 82 sách toán VNEN lớp 8 tập 2
- Giải câu 5 trang 100 sách toán VNEN lớp 8 tập 2
- Giải câu 1 trang 84 sách toán VNEN lớp 8 tập 2
- Giải câu 1 trang 28 sách toán VNEN lớp 8 tập 2
- Giải câu 1 trang 80 sách toán VNEN lớp 8 tập 2











