Đáp án câu 5 đề 10 kiểm tra học kì II toán 8

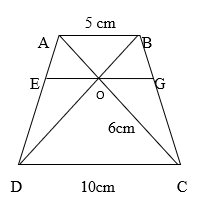
Câu 5. Cho hình thang ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Qua O kẻ đường thẳng song song với AB, cắt AD và BC theo thứ tự ở E và G.

a) Chứng minh : = $OB.OC$

b) Cho AB = 5cm, CD = 10 cm và OC = 6 cm. Hãy tính OA, OE.

c) Chứng minh rằng: = $\frac{1}{OG}$ = $\frac{1}{AB}+\frac{1}{CD}$

Bài làm:

Câu 5

a) ∆AOB∼∆COD (g.g)

= $\frac{OB}{OD}\ \Rightarrow OA.OD$ = $OC.PB$

b) Từ câu a suy ra = $\frac{OB}{OD}$ = $\frac{AB}{CD}$

= $\frac{5}{10}$

= $\frac{6.5}{10}$ = $3$cm

Do OE DC nên theo hệ quả định lí Talet:

= $\frac{AO}{AC}$ = $\frac{EO}{DC}$

\frac{EO}{10}$

= $\frac{3.10}{9}$ = $\frac{30}{9}$ = $\frac{10}{3}$ cm

c) OE AB, theo hệ quả định lý Talet ta có: $\frac{OE}{AB}$ = $\frac{DE}{DA}\left(1\right)$

* OE CB, theo hệ quả định lý Talet ta có: $\frac{OE}{DC}$ = $\frac{AE}{DA}\left(2\right)$

Cộng vế với vế của (1) và (2) ta được: = $\frac{DE}{DA}+\frac{AE}{DA}$ = $1$

= $1$ hay $\frac{1}{OE}$ = $\frac{1}{AB}+\frac{1}{CD}$

Chứng minh tương tự ta có = $\frac{1}{AB}+\frac{1}{DC}$