Giải Câu 10 Bài 2: Định lí đảo và hệ quả của định lí Ta-lét sgk Toán 8 tập 2 Trang 63

Câu 10: Trang 63 - SGK Toán 8 tập 2

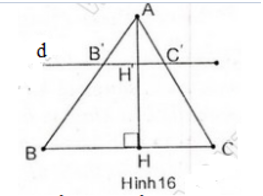
Tam giác ABC có đường cao AH. Đường thẳng d song song với BC, cắt các cạnh AB,AC và đường cao AH theo thứ tự tại các điểm B', C' và H'(h.16)

a) Chứng minh rằng: = $\frac{B^{\prime }{C}^{\prime }}{BC}$.

b) Áp dụng: Cho biết AH' = AH và diện tích tam giác ABC là 67.5 cm²

Tính diện tích tam giác AB'C'.

Bài làm:

a) Chứng minh

Vì B'C' // với BC (gt) => (Áp dụng định lí Ta-lét trong tam giác ABC)

Trong ∆ABH có BH' // BH (gt) =>

Từ (1) và (2) =>

b) B'C' // BC mà AH ⊥ BC nên AH' ⊥ B'C' hay AH' là đường cao của tam giác AB'C'.

Ta có: AH' = AH (gt) => .

Áp dụng kết quả câu a): = $\frac{A{H}^{\prime }}{AH}$ = $\frac{1}{3}$ =>

=> S_AB’C’=

=>S_AB’C’= (

mà S_ABC= = 67,5 cm²

Vậy S_AB’C’= = 7,5 cm²