Giải câu 13 bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây sgk Toán Hình 9 tập 1 Trang 106

Câu 13: Trang 106 - sgk toán 9 tập 1

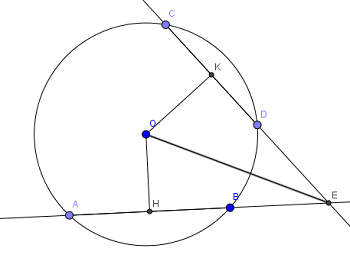
Cho đường tròn (O) có các dây AB và CD bằng nhau, các tia AB và CD cắt nhau tại điểm E nằm bên ngoài đường tròn. Gọi H và K theo thứ tự là trung điểm của AB và CD. Chứng minh rằng:

a. EH = EK.

b. EA = EC.

Bài làm:

a. Vì :

HA = HB =>

KC = KD =>

Mặt khác: AB = CD => OH = OK ( hai dây bằng nhau thì cách đều tâm )

=> ( cạnh huyền - cạnh góc vuông )

=> EH = EK ( đpcm )

b) Ta có AH = KC ( một nửa của hai dây bằng nhau )

Mà : EH = EK => EH + HA = EK + KC <=> EA = EC. ( đpcm )