Giải câu 1 trang 94 toán VNEN 7 tập 2

D.E Hoạt động vận dụng và Tìm tòi, mở rộng

Câu 1: Trang 94 sách toán VNEN 7 tập 2

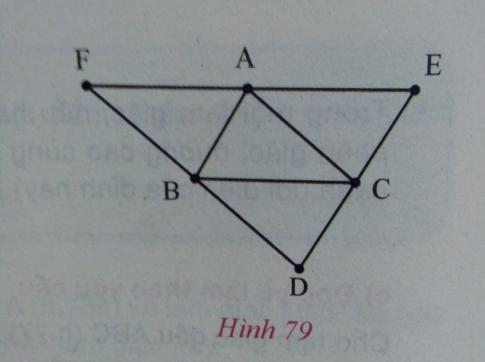
Cho tam giác ABC. Qua mỗi đỉnh A, B, C kẻ các đường thẳng song song với cạnh đối diện, chúng cắt nhau tạo thành tam giác DEF (h.79).

a) Chứng minh rằng A là trung điểm của EF.

b) Các đường cao của tam giác ABC tương ứng là các đường trung trực của tam giác nào?

Bài làm:

a) Xét tam giác ABC và tam giác ACE:

- AC là cạnh chung

- = $\widehat{CAE}$ (so le trong, AE //BC)

- = $\widehat{ACE}$ (so le trong, CE //AB)

Do đó: = $\mathrm{\Delta }CEA$ (g.c.g)

=> AE = BC (1)

Xét và $\mathrm{\Delta }ABF$ có:

- = $\widehat{BAF}$ (so le trong, BE //AC)

- = $\widehat{ABF}$ (so le trong, BF //AC)

- AC là cạnh chung

Do đó: = $\mathrm{\Delta }BAF$ (g.c.g)

=> AF = BC (2)

Từ (1) và (2) suy ra: AE = AF.

Vậy A là trung điểm của EF.

b) Kẻ AH vuông góc với BC

EF // BC (gt)

=> AH vuông góc với EF

AE = AF (chứng minh trên)

Vậy đường cao AH là đường trung trực của EF.

Chứng minh tương tự câu a, ta có B là trung điểm DF và DF // AC nên đường cao kẻ từ đỉnh B của tam giác ABC là đường trung trực DF.

Ta có C là trung điểm của DE và DE // AB nên đường cao kẻ từ đỉnh C của ∆ABC là đường trung trực của DE.