Giải câu 2 bài: Khái niệm về khối đa diện
Bài 2 :Trang 12-sgk hình học12
Chứng minh rằng một đa diện mà mỗi đỉnh của nó đều là đỉnh chung của một số lẻ mặt thì tổng số các đỉnh của nó phải là một số chẵn. Cho ví dụ.
Bài làm:
Gọi D là số đỉnh của đa diện và mỗi đỉnh của nó là đỉnh chung của một số lẻ (2n+1) mặt thì tổng số mặt của nó là (2n+1)D.
Vì mỗi cạnh là chung cho hai mặt nên số cạnh của đa diện là ![]() .
.
Vì C là số nguyên nên (2n+1)D chia hết cho 2. Mà (2n+1) là số lẻ nên D phải chia hết cho 2 hay D là số chẵn.
Vậy tổng số đỉnh của nó phải là một số chẵn.
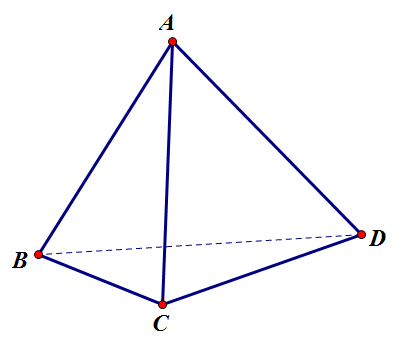
Ví dụ: Tứ diện có 4 đỉnh, mỗi đỉnh là đỉnh chung của 3 mặt.
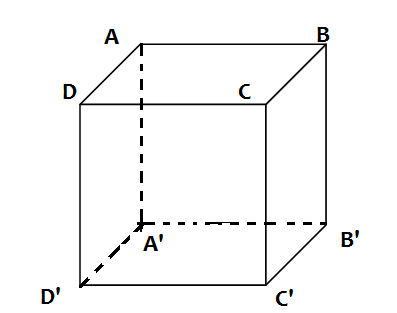
Hình lập phương có 8 đỉnh, mỗi đỉnh là đrinh chung của 3 mặt.
Xem thêm bài viết khác
- Giải câu 4 bài: Khái niệm về khối đa diện
- Giải bài 1: Khái niệm về mặt tròn xoay
- Giải câu 9 bài: Phương trình mặt phẳng
- Giải bài: Ôn tập chương III - phương pháp tọa độ trong không gian
- Giải câu 1 bài: Khái niệm về khối đa diện
- Giải bài 1: Khái niệm về khối đa diện
- Giải câu 6 bài: Phương trình mặt phẳng
- Giải câu 9 bài: Ôn tập chương III
- Giải câu 6 bài: Khái niệm về thể tích của khối đa diện
- Giải bài 1: Hệ tọa độ trong không gian
- Giải câu 6 bài: Ôn tập chương I: Khối đa diện
- Giải câu 1 bài: Khái niệm về thể tích của khối đa diện











