Giải câu 4 bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số

Câu 4: Trang 44 - sgk giải tích 12

Bằng cách khảo sát hàm số, hãy tìm số nghiệm của các phương trình sau:

a)

b)

c)

Bài làm:

a) (1)

Số nghiệm của phương trình (1) là số giao điểm của đồ thị hàm số $y =x^{3} - 3x^{2} + 5 và trục hoành ( y = 0 ).

Xét hàm số ta có:

• TXĐ: D = R
• Sự biến thiên:

Ta có:

=>

• Giới hạn:

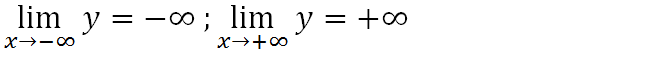
• Bảng biến thiên:

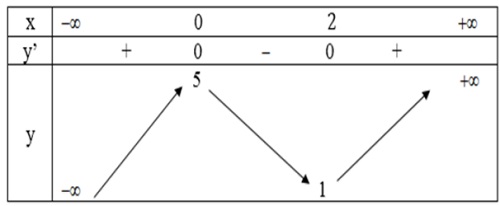
• Đồ thị:

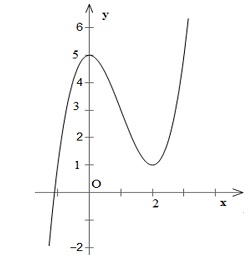
=> Đồ thị hàm số chỉ cắt trục hoành tại 1 điểm duy nhất.

=> Phương trình chỉ có 1 nghiệm.

b)

<=> (2)

Số nghiệm của phương trình (2) là số giao điểm của đồ thị hàm số và đường thẳng $y=-2$.

Xét hàm số

• TXĐ: D = R
• Sự biến thiên:

Ta có:

=>

• Giới hạn:

• Bảng biến thiên:

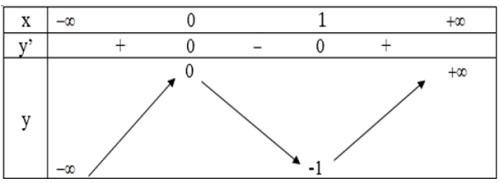
• Đồ thị:

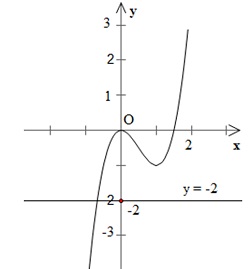
=> Đồ thị hàm số chỉ cắt đường thẳng $y=-2$ tại 1 điểm duy nhất.

=> Phương trình chỉ có 1 nghiệm.

c) (3)

Số nghiệm của phương trình (3) là số giao điểm của đồ thị hàm số và đường thẳng $y=-1$.

Xét hàm số ta có:

• TXĐ: D = R
• Sự biến thiên:

Ta có:

=>

• Giới hạn:

• Bảng biến thiên:

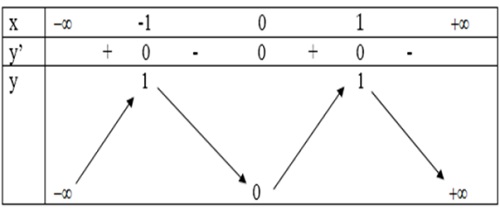
• Đồ thị:

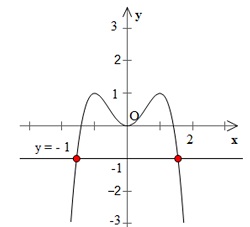
=> Đồ thị hàm số cắt đường thẳng $y=-$1 tại hai điểm.

=> Phương trình có hai nghiệm phân biệt.