Giải Câu 5 Bài: Ôn tập cuối năm sgk Hình học 10 Trang 99

Câu 5: Trang 99 - SGK Hình học 10

Chứng minh rẳng trong mọi tam giác ABC ta đều có:

a)

b)

c)

Bài làm:

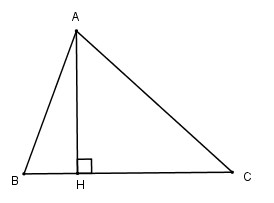
Tam giác có: $AB=c;AC=b;BC=a$, bán kính đường tròn ngoại tiếp là $R$, $AH\perp BC;AH=h_a$.

a) Trong tam giác , theo định lí cosin ta có:

Suy ra:

Vậy

b) Trong tam giác , theo định lí sin:

\(\eqalign{
& {a \over {\sin A}} = {b \over {{\mathop{\rm sinB}\nolimits} }} = {c \over {\sin C}} = 2R \cr
& \Rightarrow \sin A = {a \over {2R}},\sin B = {b \over {2R}},\sin C = {c \over {2R}} \cr} \)

Ta có:

\(\eqalign{& \sin B\cos C + \sin C\cos B \cr & = {b \over {2R}}.{{{a^2} + {b^2} - {c^2}} \over {2ab}} + {c \over {2R}}.{{{a^2} + {c^2} - {b^2}} \over {2ac}} \cr
& = {a \over {2R}} = \sin A \cr} \)

c) Ta lại có:

mà

Thế vào (2) ta được: